Como construir uma árvore de classificação no R
Essa é uma tradução. O artigo original pode ser visto aqui. Vou pular direto para a construção de uma árvore de classificação no e explicar os conceitos ao longo do caminho. Usaremos o banco de dados da íris, que mede em centímetros as variáveis comprimento e largura da pétala e comprimento e largura da pétala, respectivamente, para 50 flores de três espécies diferentes da base de dados.
[1] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" "Species" 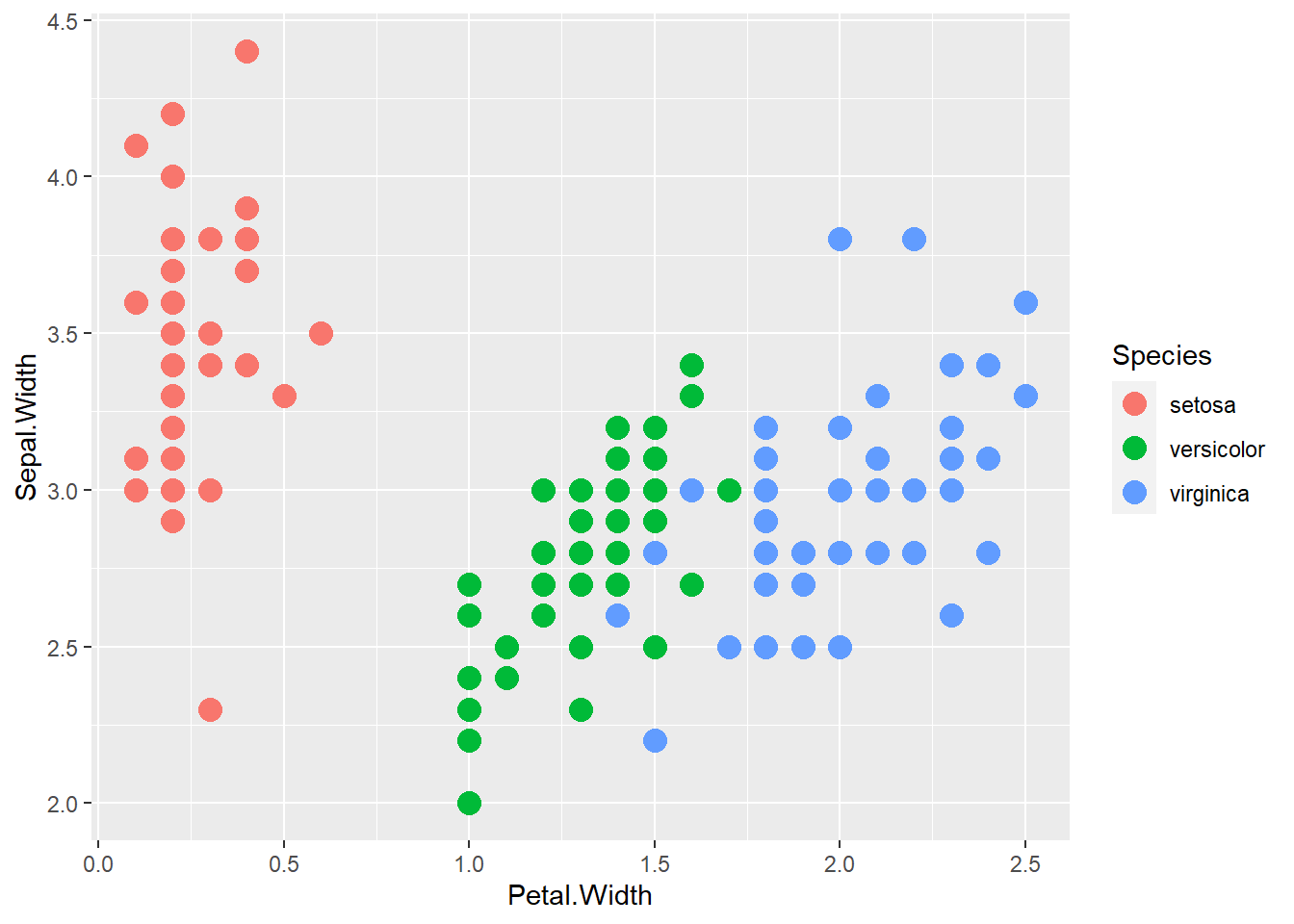
Diferentes espécies têm larguras características de sépalas e pétalas.
A idéia básica de uma árvore de classificação é começar primeiro com todas as variáveis em um grupo; imagine todos os pontos no gráfico de dispersão acima. Em seguida, encontre alguma característica que melhor separe os grupos; por exemplo, a primeira divisão pode estar perguntando se as larguras das pétalas são menores ou iguais a 0,8. Continue esse processo até que as partições sejam suficientemente homogêneas ou muito pequenas.
Classification tree:
tree(formula = Species ~ Sepal.Width + Petal.Width, data = iris)
Number of terminal nodes: 5
Residual mean deviance: 0.204 = 29.57 / 145
Misclassification error rate: 0.03333 = 5 / 150 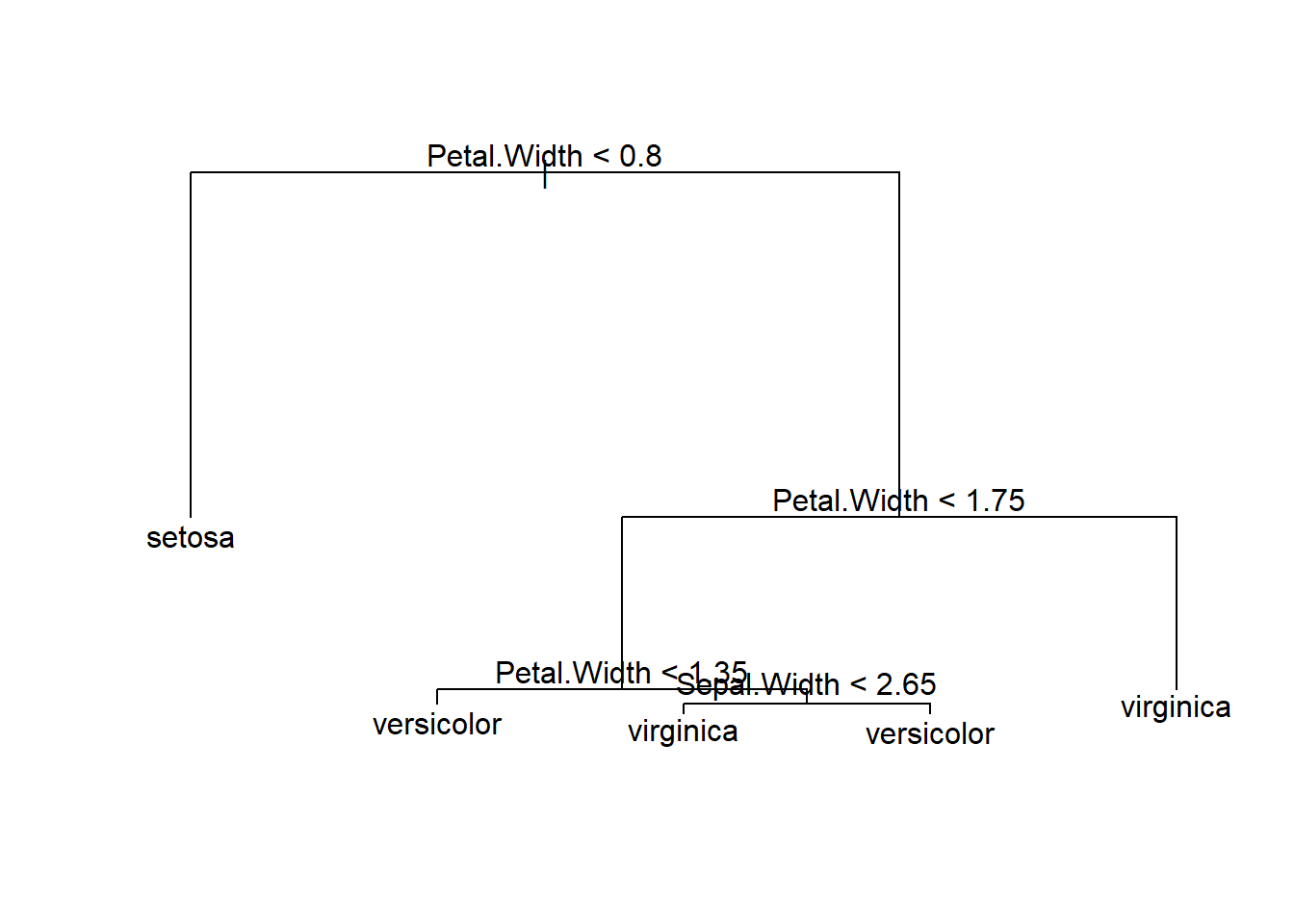
Uma árvore de classificação mostrando cada nó.
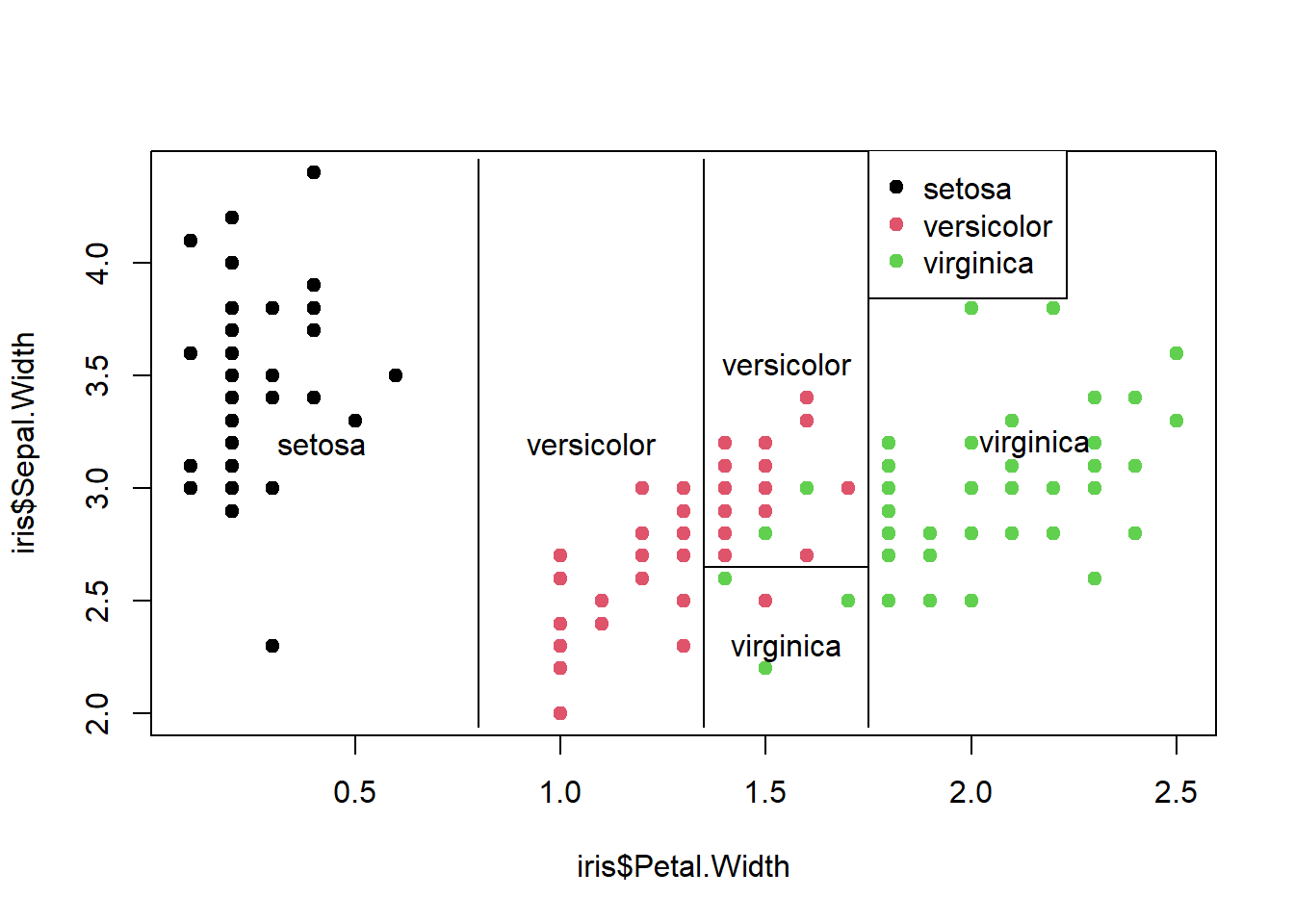
As partições são definidas pela árvore de classificação acima. Por exemplo, o primeiro nó divide todas as espécies com largura de pétala <0,8 como setosa. Em seguida, todas as espécies com largura de pétala> 1,75 são virgínicas e assim por diante.
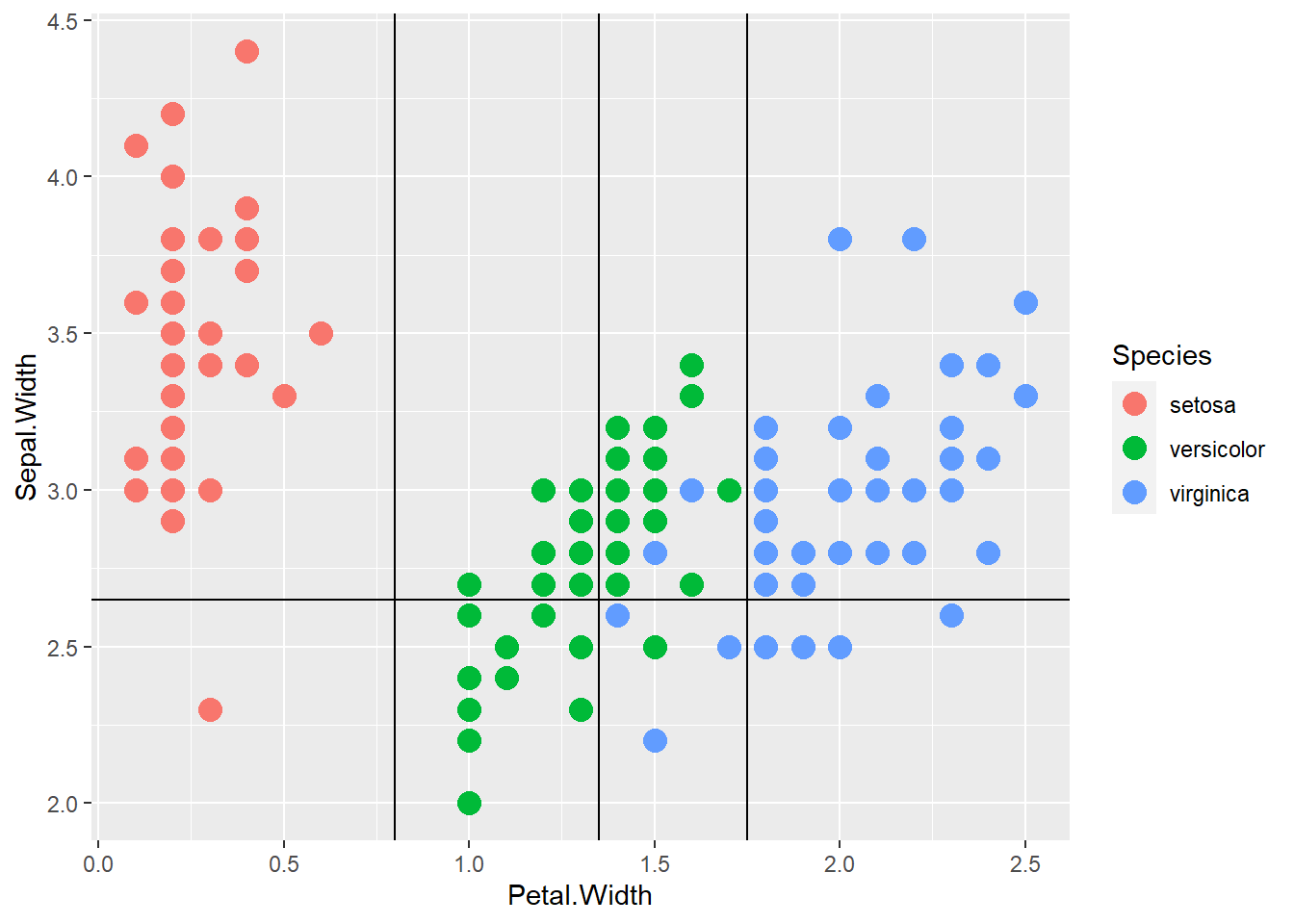
Eu contei 3 classificações incorretas, no entanto, a partir da saída do resumo (árvore1), havia 5. Refiz as partições usando ggplot2, mas ainda observo apenas 3.
Usando mais variáveis
Usei duas variáveis acima, Petal.Width e Sepal.Width para ilustrar o processo de classificação. Podemos incluir todas as quatro variáveis no processo de classificação:
Classification tree:
tree(formula = Species ~ Sepal.Width + Sepal.Length + Petal.Length +
Petal.Width, data = iris)
Variables actually used in tree construction:
[1] "Petal.Length" "Petal.Width" "Sepal.Length"
Number of terminal nodes: 6
Residual mean deviance: 0.1253 = 18.05 / 144
Misclassification error rate: 0.02667 = 4 / 150 Temos uma taxa de erro de classificação incorreta ligeiramente mais baixa (0,02667) e aqui está a aparência da árvore de classificação:

Vamos verificar alguns destes subconjuntos do conjunto de dados da íris:
[1] setosa setosa setosa setosa setosa setosa setosa setosa setosa setosa
[11] setosa setosa setosa setosa setosa setosa setosa setosa setosa setosa
[21] setosa setosa setosa setosa setosa setosa setosa setosa setosa setosa
[31] setosa setosa setosa setosa setosa setosa setosa setosa setosa setosa
[41] setosa setosa setosa setosa setosa setosa setosa setosa setosa setosa
Levels: setosa versicolor virginica
[1] 50
[1] versicolor virginica virginica virginica virginica virginica
[7] virginica virginica virginica virginica virginica virginica
[13] virginica virginica virginica virginica virginica virginica
[19] virginica virginica virginica virginica virginica virginica
[25] virginica virginica virginica virginica virginica virginica
[31] virginica virginica virginica virginica virginica virginica
[37] virginica virginica virginica virginica virginica virginica
[43] virginica virginica virginica virginica
Levels: setosa versicolor virginica
[1] 46
[1] versicolor versicolor virginica virginica virginica virginica
Levels: setosa versicolor virginica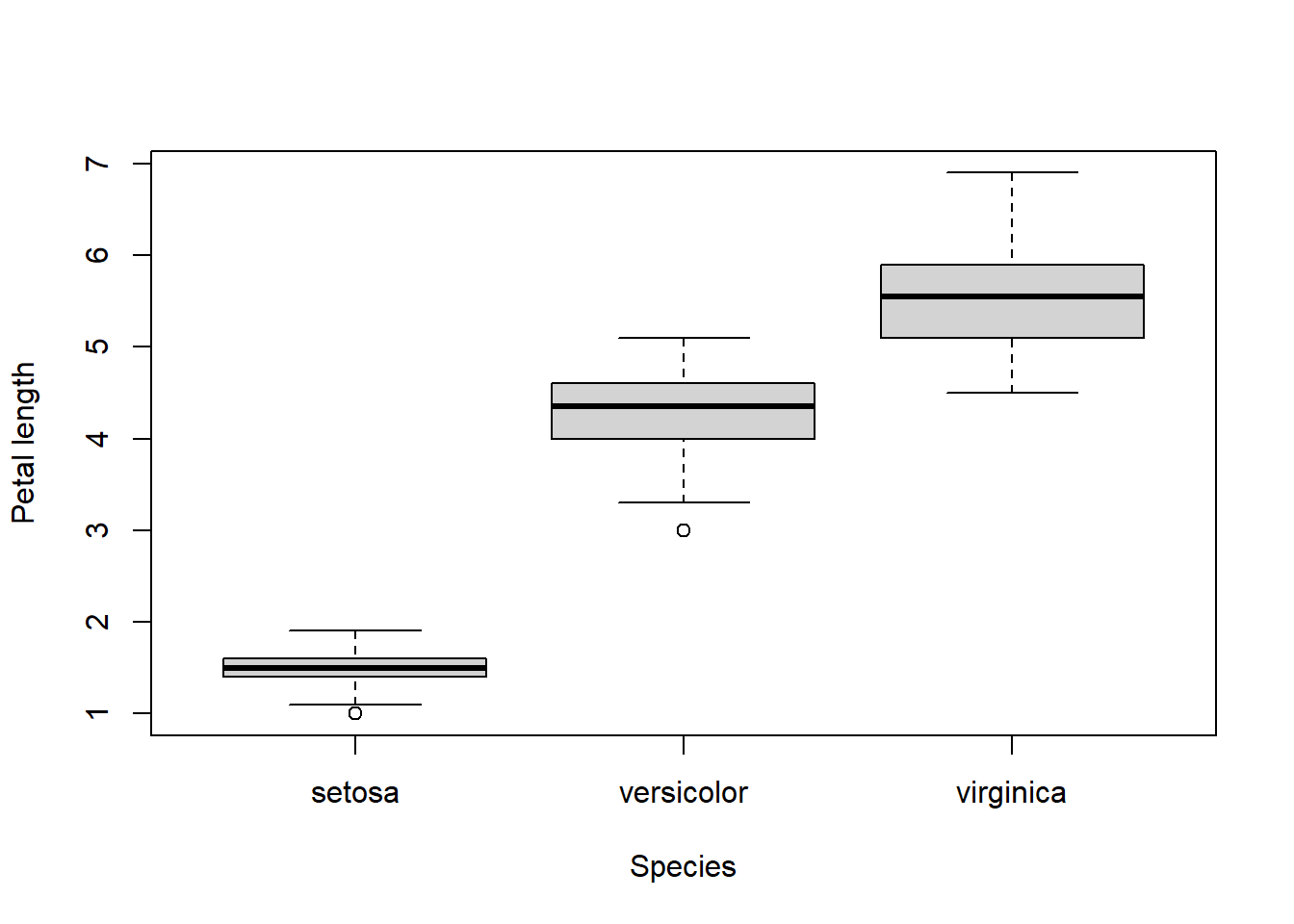
Podemos facilmente distinguir espécies de setosa pelo comprimento das pétalas.
Árvores de classificação mais bonitas no usando o pacote rpart
n= 150
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 150 100 setosa (0.33333333 0.33333333 0.33333333)
2) Petal.Length< 2.45 50 0 setosa (1.00000000 0.00000000 0.00000000) *
3) Petal.Length>=2.45 100 50 versicolor (0.00000000 0.50000000 0.50000000)
6) Petal.Width< 1.75 54 5 versicolor (0.00000000 0.90740741 0.09259259) *
7) Petal.Width>=1.75 46 1 virginica (0.00000000 0.02173913 0.97826087) *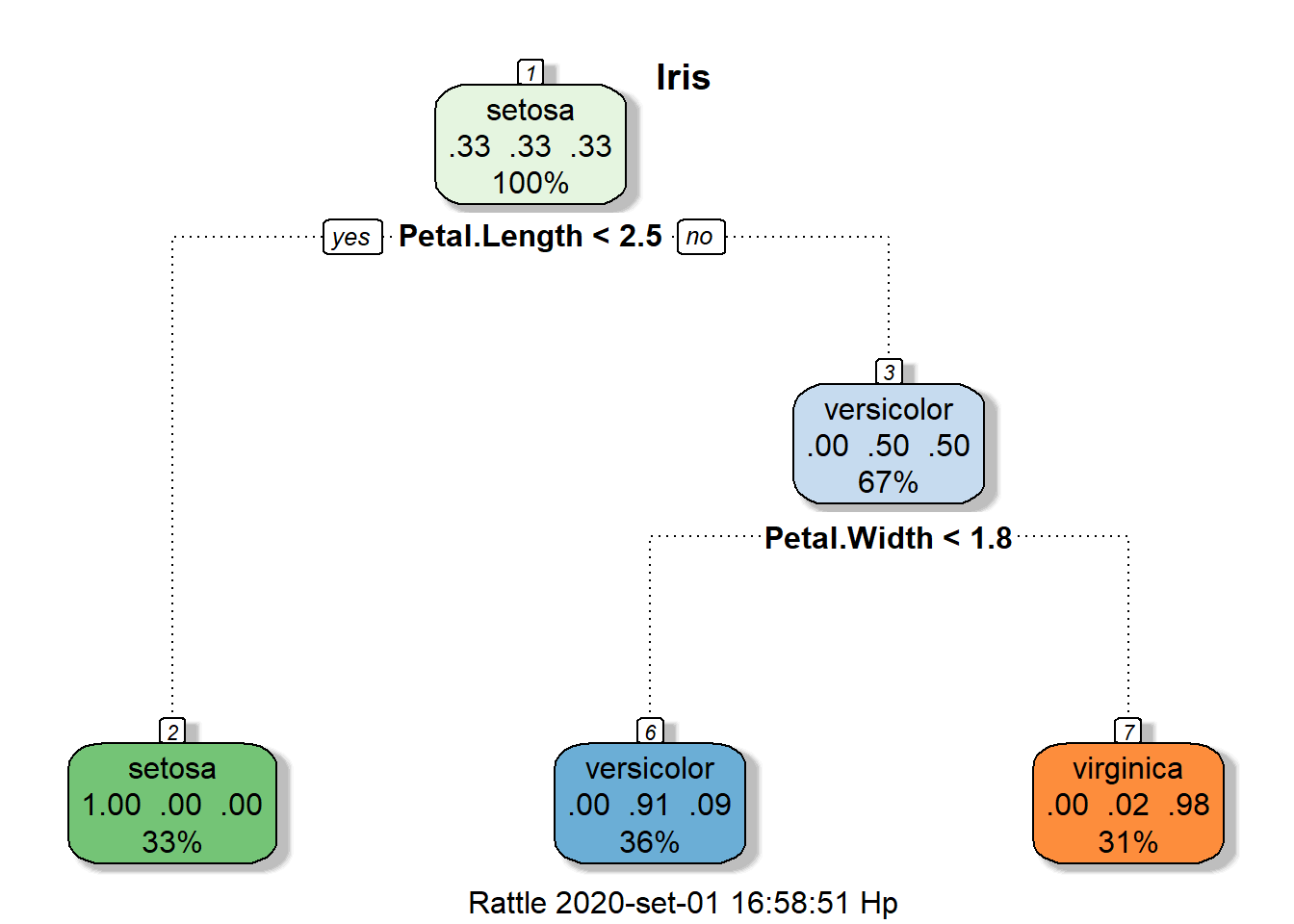
A mesma história acima, mas uma árvore de classificação mais sofisticada.
Conclusões
Uma das desvantagens das árvores de decisão pode ser a adaptação excessiva, ou seja, a criação contínua de partições para atingir uma população relativamente homogênea. Esse problema pode ser aliviado pela poda da árvore, que basicamente remove as decisões de baixo para cima. Outra maneira é combinar várias árvores e obter um consenso, o que pode ser feito através do random forest.
