Introdução à Análise de Correspondência
Análise Correspondência
Variáveis nominais
Análise Multivariada
Introdução
Você não precisa usar o R… pode usar o Python também.
Análise de Correspondência
A análise de correspondência (CA) é uma técnicas multivariadas que nos ajudam a resumir os padrões sistemáticos de variações nos dados. A concepção geral é semelhante à análise de componentes principais, diferenciando-se desta, entre outros aspectos, por permitir a inclusão de variáveis qualitativas (ou dados categóricos). Como a análise de componentes principais, ela fornece uma solução para resumir e visualizar o conjunto de dados em gráficos de duas dimensões.
Como no análise de componentes principais, os autovalores fornecem informações sobre a variabilidade nos dados. As coordenadas da linha fornecem informações sobre a estrutura das linhas na tabela analisada. As coordenadas da coluna fornecem informações sobre a estrutura das colunas na tabela analisada.
Os dados
Usaremos o banco de dados author que já vem com o pacote “ca”. É uma matriz de dados que contém as contagens das 26 letras do alfabeto (colunas da matriz) para 12 romances diferentes (linhas da matriz). Cada linha contém contagens de letras em uma amostra de texto de cada obra, excluindo nomes próprios.
library(ca)
package ‘ca’ was built under R version 4.0.2
# apply ca
data(author)
head(author)
## a b c d e f g h i j k l m
## three daughters (buck) 550 116 147 374 1015 131 131 493 442 2 52 302 159
## drifters (michener) 515 109 172 311 827 167 136 376 432 8 61 280 146
## lost world (clark) 590 112 181 265 940 137 119 419 514 6 46 335 176
## east wind (buck) 557 129 128 343 996 158 129 571 555 4 76 291 247
## farewell to arms (hemingway) 589 72 129 339 866 108 159 449 472 7 59 264 158
## sound and fury 7 (faulkner) 541 109 136 228 763 126 129 401 520 5 72 280 209
## n o p q r s t u v w x y z
## three daughters (buck) 534 516 115 4 409 467 632 174 66 155 5 150 3
## drifters (michener) 470 561 140 4 368 387 632 195 60 156 14 137 5
## lost world (clark) 403 505 147 8 395 464 670 224 113 146 13 162 10
## east wind (buck) 479 509 92 3 413 533 632 181 68 187 10 184 4
## farewell to arms (hemingway) 504 542 95 0 416 314 691 197 64 225 1 155 2
## sound and fury 7 (faulkner) 471 589 84 2 324 454 672 247 71 160 11 280 1Para fazer o Análise de Correspondência, precisamos:
# apply ca
ca1 <-ca(author)
# sqrt of eigenvalues
ca1$sv
## [1] 0.08754348 0.06073157 0.04910398 0.03718655 0.03164900 0.02689484
## [7] 0.02566321 0.02132718 0.01933685 0.01621904 0.01063892
plot(ca1)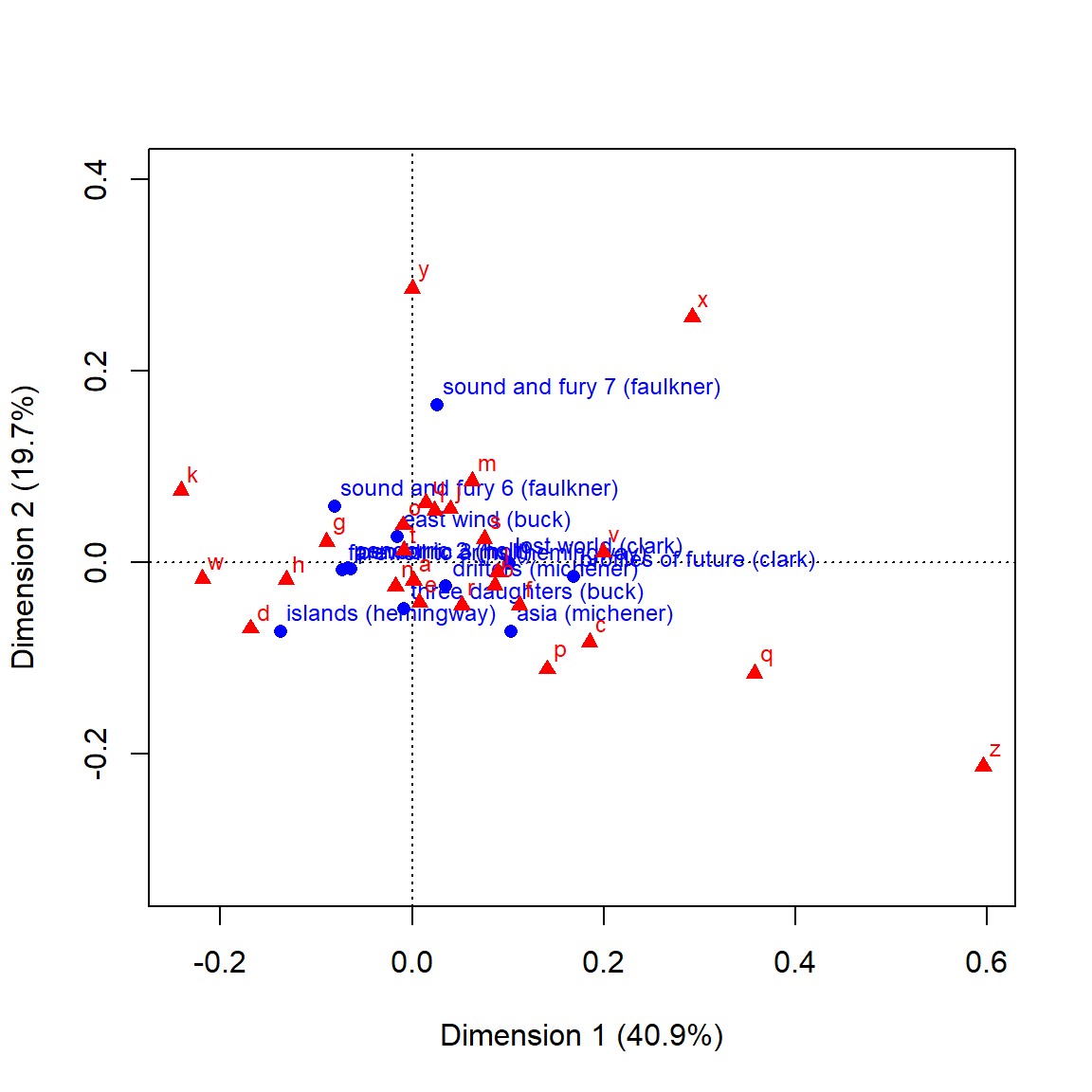
Podemos usar também o pacote amap
library(amap)
# apply CA
ca2 <- afc(author)
# eigenvalues
ca2$eig
## [1] 0.1841506355308312 0.1345567686719785 0.1035679129627933 0.0874399854189873
## [5] 0.0620715229449494 0.0346987842026542 0.0346987842026542 0.0298474931530984
## [9] 0.0298474931530984 0.0241898038331218 0.0177074035132544 0.0042882697696728
## [13] 0.0000000020341526 0.0000000004690142 0.0000000004690142 0.0000000009408433
## [17] 0.0000000006619892 0.0000000006619892 0.0000000003302806 0.0000000003302806
## [21] 0.0000000007660766 0.0000000003776303 0.0000000003776303 0.0000000001918946
## [25] 0.0000000001918946 0.0000000001337226
# column coordinates
head(ca2$loadings)
## Comp 1 Comp 2 Comp 3 Comp 4 Comp 5 Comp 6
## a 0.003021805 0.020612471 0.061491650 0.06195169 0.05277265 0.043411228
## b -0.092480077 0.008900985 -0.091344746 -0.07466805 -0.08659821 -0.022568685
## c -0.178709976 0.055824156 0.098703814 0.13197550 0.15376077 0.064301539
## d 0.073137989 0.003039285 0.156073522 -0.34173594 -0.29959159 0.269559733
## e -0.019220675 0.012044163 -0.002028131 -0.02438577 -0.18620776 0.007124395
## f -0.106716718 0.055965712 -0.071859158 0.04725359 -0.06634236 -0.096594194
## Comp 7 Comp 8 Comp 9 Comp 10 Comp 11 Comp 12
## a 0.043411228 -0.06499409 -0.06499409 0.07583377 0.06867065 -0.09411071
## b -0.022568685 -0.03961747 -0.03961747 0.08500085 0.10155707 0.28316254
## c 0.064301539 -0.15065932 -0.15065932 0.26829725 0.40200772 -0.01904581
## d 0.269559733 -0.19360223 -0.19360223 0.08524852 0.15203209 0.26842013
## e 0.007124395 0.04881236 0.04881236 -0.17417766 -0.11241046 -0.13982175
## f -0.096594194 0.07173540 0.07173540 0.19381495 0.06159557 0.28308605
## Comp 13 Comp 14 Comp 15 Comp 16 Comp 17 Comp 18
## a 0.20567775 0.4721497 0.4721497 -0.28537432 0.2721303 0.2721303
## b -0.03666870 -0.2146803 -0.2146803 0.11343296 -0.1243297 -0.1243297
## c 0.35904377 0.1226989 0.1226989 0.01781606 0.1082090 0.1082090
## d 0.03421843 -0.2049718 -0.2049718 -0.34190986 -0.3788812 -0.3788812
## e -0.07566568 0.1210939 0.1210939 -0.07270544 0.1265331 0.1265331
## f 0.02289783 -0.1099741 -0.1099741 -0.38805643 -0.2324474 -0.2324474
## Comp 19 Comp 20 Comp 21 Comp 22 Comp 23 Comp 24
## a -0.4497326 -0.4497326 -0.76830645 -0.42052797 -0.42052797 -0.17788618
## b 0.1913499 0.1913499 0.22611294 0.10290472 0.10290472 0.01092377
## c -0.1314393 -0.1314393 -0.01929074 -0.08109856 -0.08109856 -0.01783082
## d 0.3926394 0.3926394 0.11444973 0.22803928 0.22803928 -0.03366907
## e -0.1754112 -0.1754112 -0.06054662 -0.18622533 -0.18622533 -0.04366527
## f 0.2252146 0.2252146 0.04041559 0.21550164 0.21550164 0.15195986
## Comp 25 Comp 26
## a -0.17788618 0.24033710
## b 0.01092377 -0.07016318
## c -0.01783082 0.11983643
## d -0.03366907 -0.17323723
## e -0.04366527 0.09777100
## f 0.15195986 -0.16993857
# plot
plot(ca2)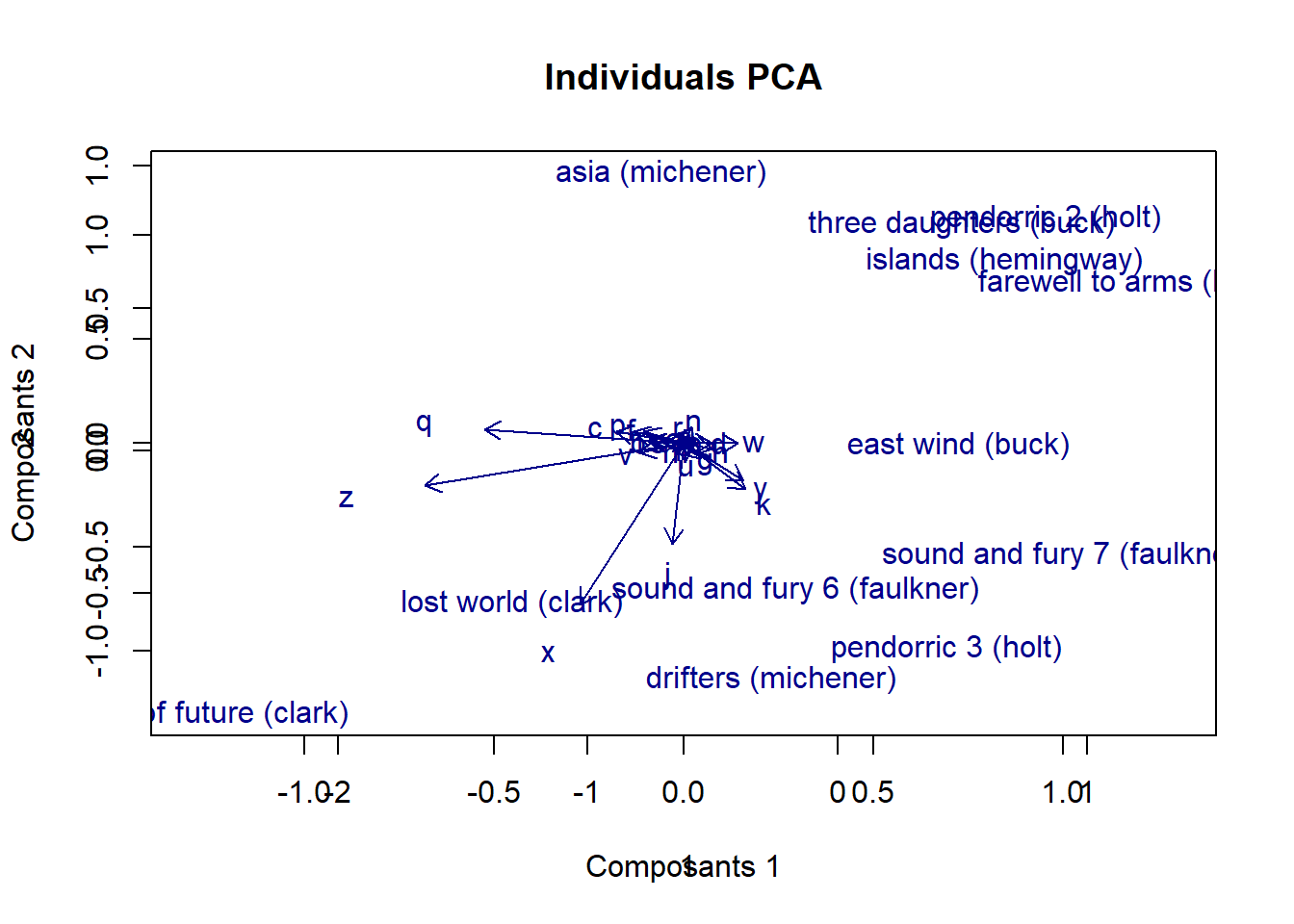
O pacote FactoMineR faz o mesmo procedimento. Esse pacote fornece muitos resultados mais detalhados e ferramentas de avaliação.
# CA with function CA
library(FactoMineR)
# apply CA
ca3 <- CA(author, graph = FALSE)
# matrix with eigenvalues
ca3$eig
## eigenvalue percentage of variance cumulative percentage of variance
## dim 1 0.0076638606 40.9070362 40.90704
## dim 2 0.0036883237 19.6869956 60.59403
## dim 3 0.0024112012 12.8701577 73.46419
## dim 4 0.0013828392 7.3811169 80.84531
## dim 5 0.0010016592 5.3465103 86.19182
## dim 6 0.0007233324 3.8608981 90.05271
## dim 7 0.0006586002 3.5153798 93.56809
## dim 8 0.0004548486 2.4278243 95.99592
## dim 9 0.0003739137 1.9958218 97.99174
## dim 10 0.0002630573 1.4041087 99.39585
## dim 11 0.0001131866 0.6041507 100.00000Visualização e interpretação
Vamos usar as seguintes funções [do pacote fatoextra] para ajudar na interpretação e na visualização da análise de correspondência:
- get_eigenvalue(res.ca): Extract the eigenvalues/variances retained by each dimension (axis)
- fviz_eig(res.ca): Visualize the eigenvalues
- get_ca_row(res.ca), get_ca_col(res.ca): Extract the results for rows and columns, respectively.
- fviz_ca_row(res.ca), fviz_ca_col(res.ca): Visualize the results for rows and columns, respectively.
- fviz_ca_biplot(res.ca): Make a biplot of rows and columns.
library("factoextra")
package ‘factoextra’ was built under R version 4.0.2
Carregando pacotes exigidos: ggplot2
package ‘ggplot2’ was built under R version 4.0.2
Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBa
eig.val <- get_eigenvalue(ca3)
eig.val
## eigenvalue variance.percent cumulative.variance.percent
## Dim.1 0.0076638606 40.9070362 40.90704
## Dim.2 0.0036883237 19.6869956 60.59403
## Dim.3 0.0024112012 12.8701577 73.46419
## Dim.4 0.0013828392 7.3811169 80.84531
## Dim.5 0.0010016592 5.3465103 86.19182
## Dim.6 0.0007233324 3.8608981 90.05271
## Dim.7 0.0006586002 3.5153798 93.56809
## Dim.8 0.0004548486 2.4278243 95.99592
## Dim.9 0.0003739137 1.9958218 97.99174
## Dim.10 0.0002630573 1.4041087 99.39585
## Dim.11 0.0001131866 0.6041507 100.00000Os autovalores correspondem à quantidade de informações retidas por cada eixo. As dimensões são ordenadas decrescentemente e listadas de acordo com a quantidade de variação explicada na solução. A dimensão 1 explica a maior variação na solução, seguida pela dimensão 2 e assim por diante.
A porcentagem cumulativa explicada é obtida adicionando as proporções sucessivas de variação explicadas para obter o total corrente. Por exemplo, 40,9% mais 19,6% é igual a 60,59% e assim por diante. Portanto, cerca de 73,46% da variação é explicada pelas três primeiras dimensões.
Os autovalores podem ser usados para determinar o número de eixos a serem retidos. Não existe uma “regra de ouro” para escolher o número de dimensões. Depende da pergunta da pesquisa e da necessidade do pesquisador. Por exemplo, se você estiver satisfeito com 70% do total de variações explicadas, use o número de dimensões necessárias para conseguir isso.
Um método alternativo para determinar o número de dimensões é examinar o gráfico Screeplot, que é o gráfico de autovalores ordenados do maior para o menor. O número de componentes é determinado no ponto, além do qual os valores próprios restantes são todos relativamente pequenos e de tamanho comparável.
O gráfico screeplot pode ser produzido usando a função fviz_eig() ou fviz_screeplot().
fviz_screeplot(ca3, addlabels = TRUE, ylim = c(0, 50))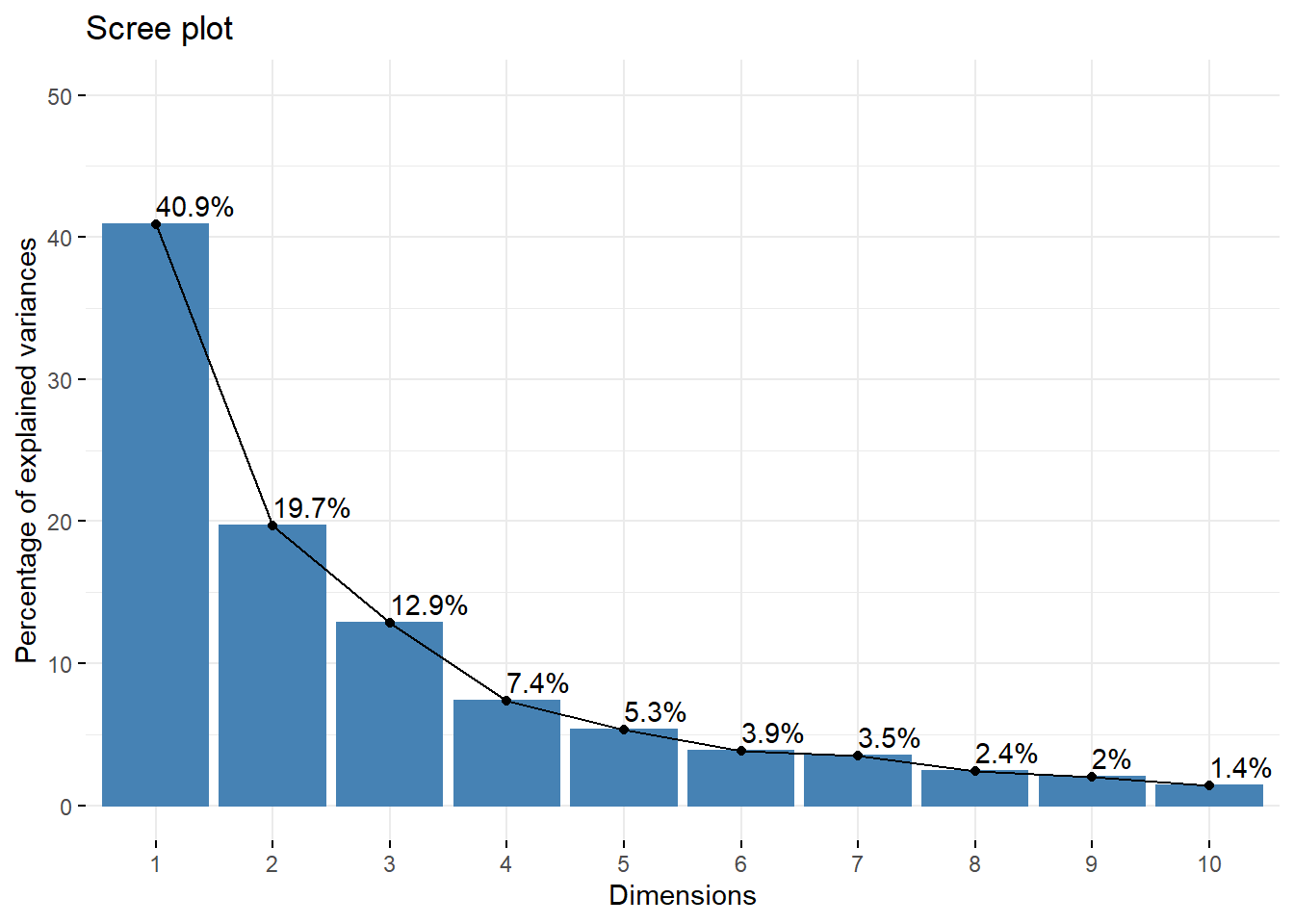
Vou colocar uma linha horizontal para sugerir um corte.
fviz_screeplot(ca3) +
geom_hline(yintercept=10, linetype=2, color="red")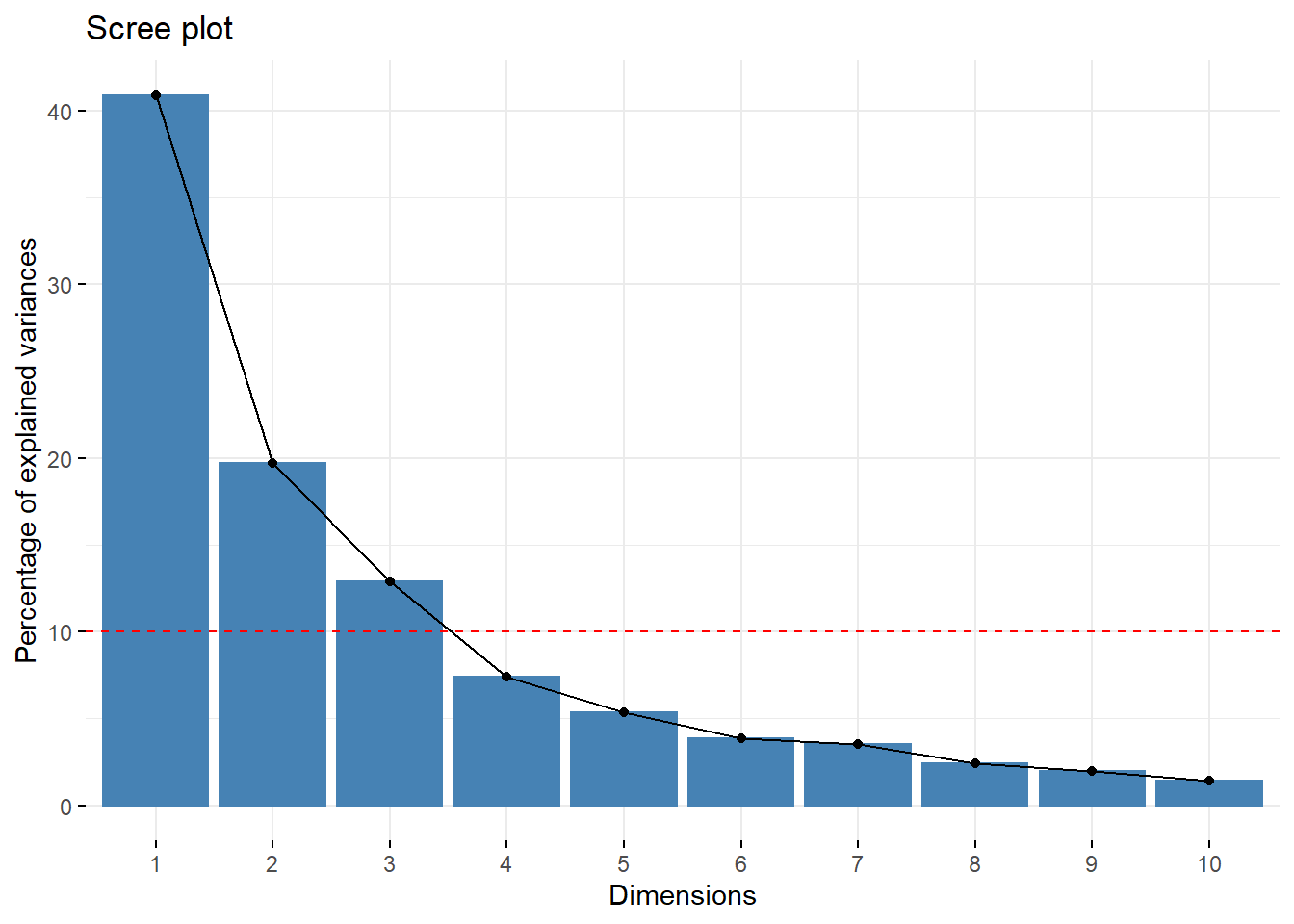
Biplot
A função fviz_ca_biplot() pode ser usada para desenhar o biplot de variáveis de linhas e colunas.
fviz_ca_biplot(ca3, repel = TRUE)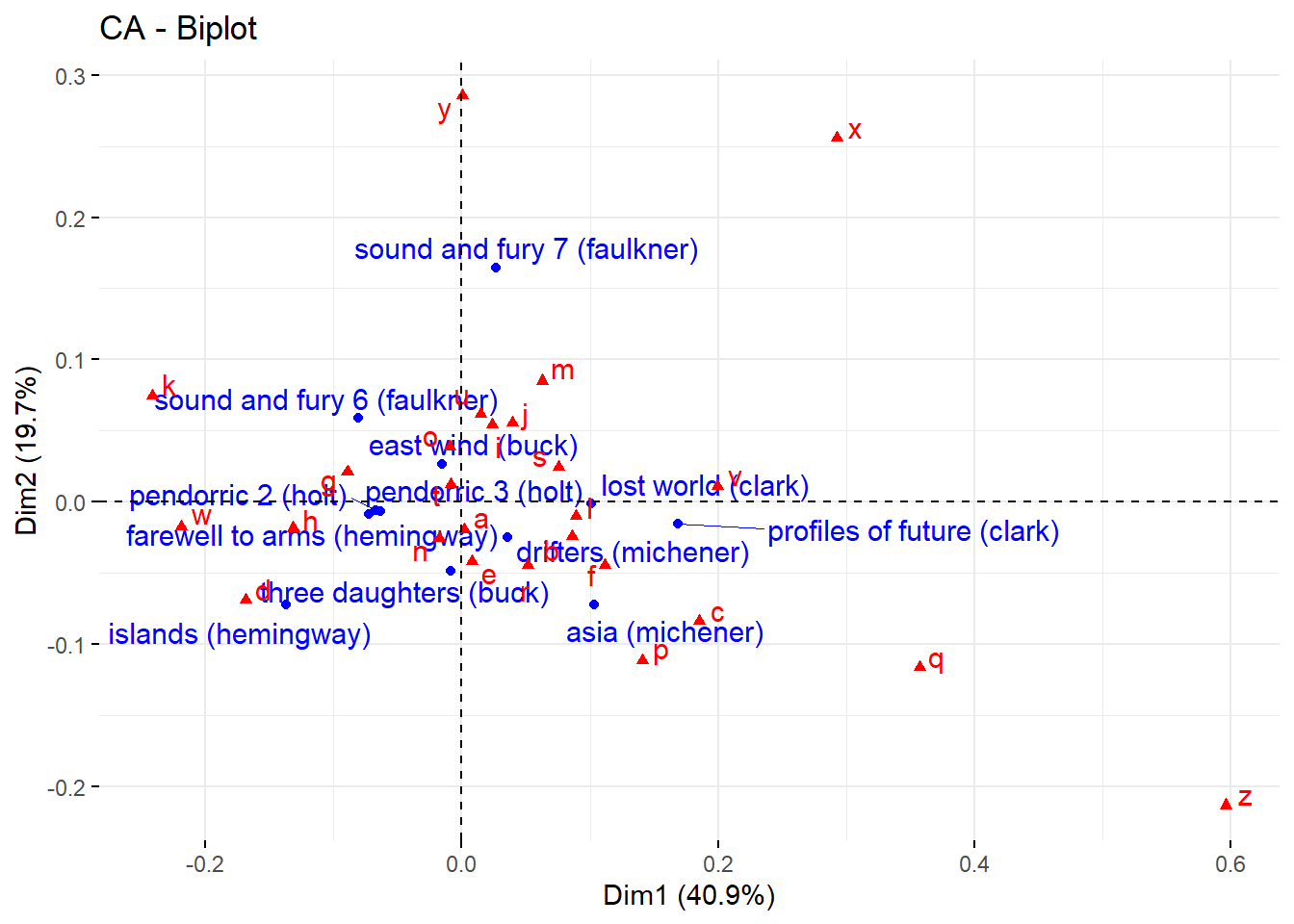
As linhas são representadas por pontos azuis e colunas por triângulos vermelhos.
A distância entre quaisquer pontos de linha ou pontos de coluna fornece uma medida de sua similaridade (ou dissimilaridade). Pontos de linha com perfil semelhante são próximos. O mesmo vale para pontos da coluna.
O som e a fúria do Faulkner, é próximo do y e o Hemingway está próximo do d. A interpretação é que o William Faulkner utiliza mais o y que o Hemingway.
Gráfico de variáveis de linha
A função get_ca_row() é usada para extrair os resultados para variáveis de linha. Esta função retorna uma lista contendo o cos2 (the squared cosine):
row <- get_ca_row(ca3)
row
## Correspondence Analysis - Results for rows
## ===================================================
## Name Description
## 1 "$coord" "Coordinates for the rows"
## 2 "$cos2" "Cos2 for the rows"
## 3 "$contrib" "contributions of the rows"
## 4 "$inertia" "Inertia of the rows"O cos2 mede o grau de associação entre linhas / colunas e um eixo específico. O cos2 dos pontos da linha pode ser extraído da seguinte maneira:
head(row$cos2)
## Dim 1 Dim 2 Dim 3 Dim 4
## three daughters (buck) 0.007285862 0.2435634733 0.266510444 0.060512923
## drifters (michener) 0.140312868 0.0674815766 0.232179622 0.061914615
## lost world (clark) 0.622830707 0.0001194593 0.018430579 0.094884079
## east wind (buck) 0.016461980 0.0494450450 0.745992597 0.008787674
## farewell to arms (hemingway) 0.351196925 0.0045496036 0.142188292 0.149054018
## sound and fury 7 (faulkner) 0.023380529 0.9043122585 0.002655727 0.023020619
## Dim 5
## three daughters (buck) 0.1350531089
## drifters (michener) 0.0008024716
## lost world (clark) 0.1088446102
## east wind (buck) 0.0656781316
## farewell to arms (hemingway) 0.0827136472
## sound and fury 7 (faulkner) 0.0031149913Os valores do cos2 são compreendidos entre 0 e 1. A soma do cos2 para linhas em todas as dimensões da CA é igual a um.
A qualidade da representação de uma linha ou coluna em n dimensões é simplesmente a soma do cosseno quadrado dessa linha ou coluna sobre as n dimensões.
Se um item de linha estiver bem representado por duas dimensões, a soma do cos2 será próxima de um. Para alguns itens de linha, são necessárias mais de duas dimensões para representar perfeitamente os dados.
# Color by cos2 values: quality on the factor map
fviz_ca_row(ca3, col.row = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE)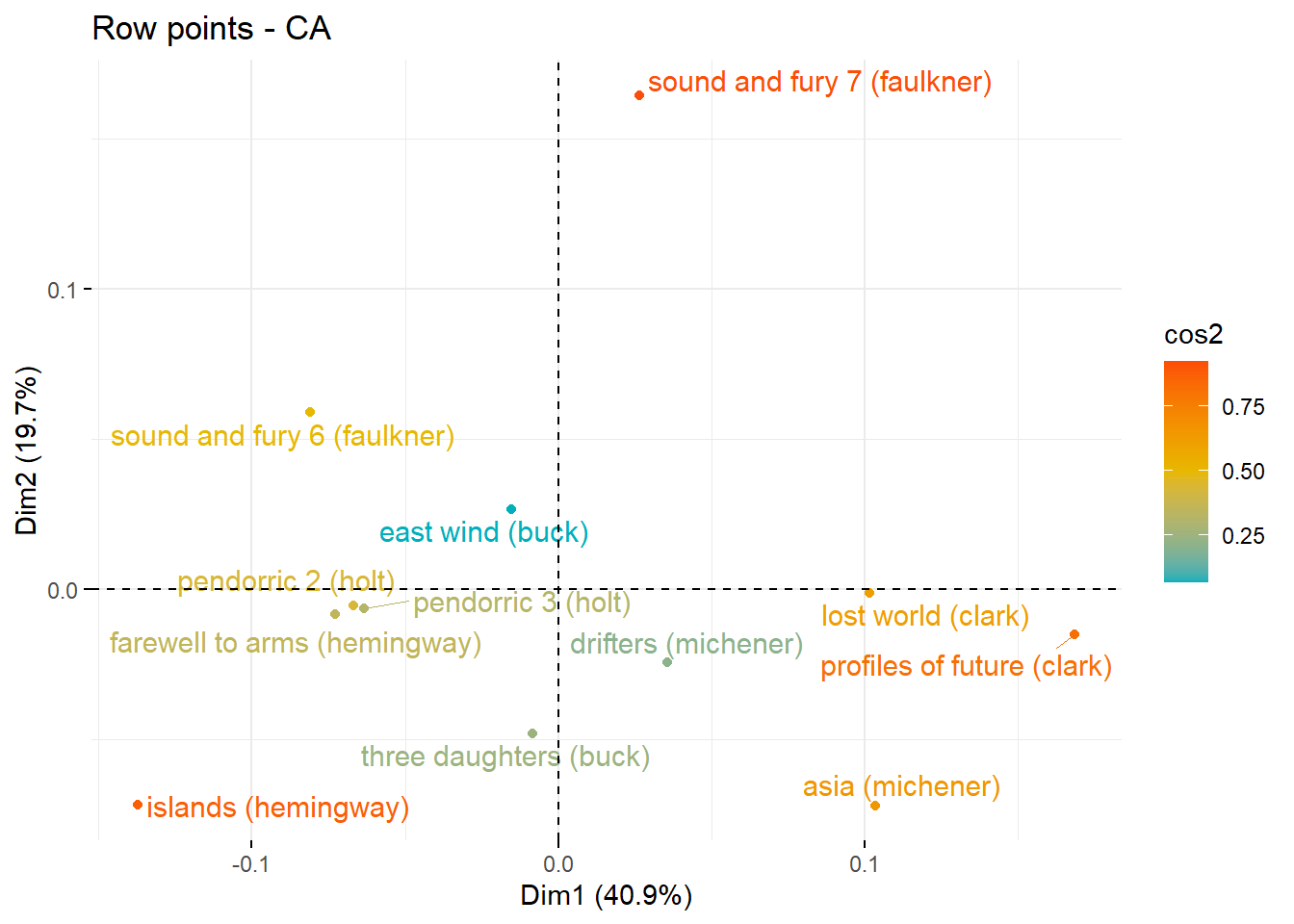
Você pode visualizar o cos2 dos pontos da linha em todas as dimensões usando o pacote corrplot:
library("corrplot")
package ‘corrplot’ was built under R version 4.0.2
corrplot 0.84 loaded
corrplot(row$cos2, is.corr=FALSE)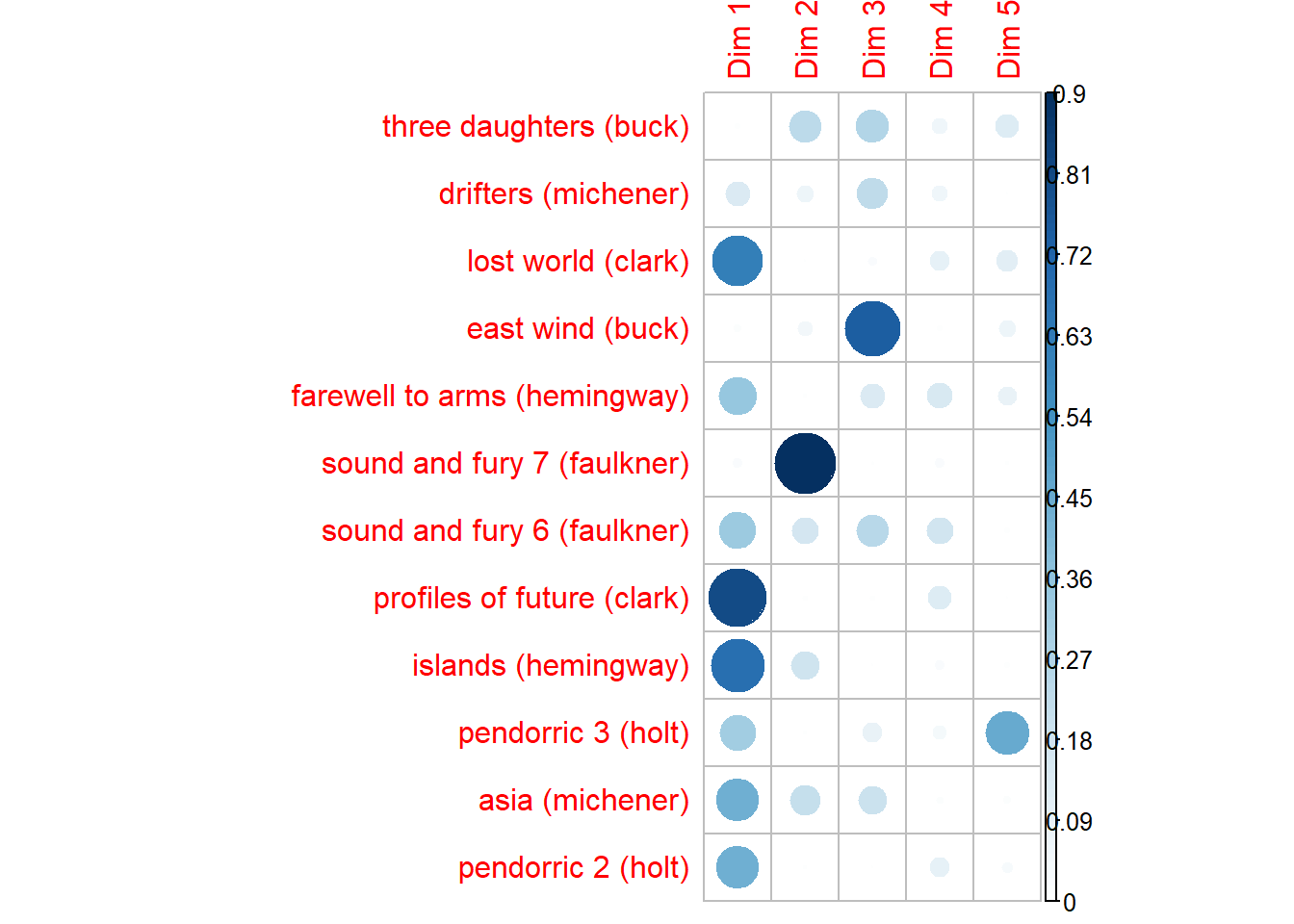
Também é possível criar um gráfico de barras das linhas cos2 usando a função fviz_cos2()
# Cos2 of rows on Dim.1 and Dim.2
fviz_cos2(ca3, choice = "row", axes = 1:2)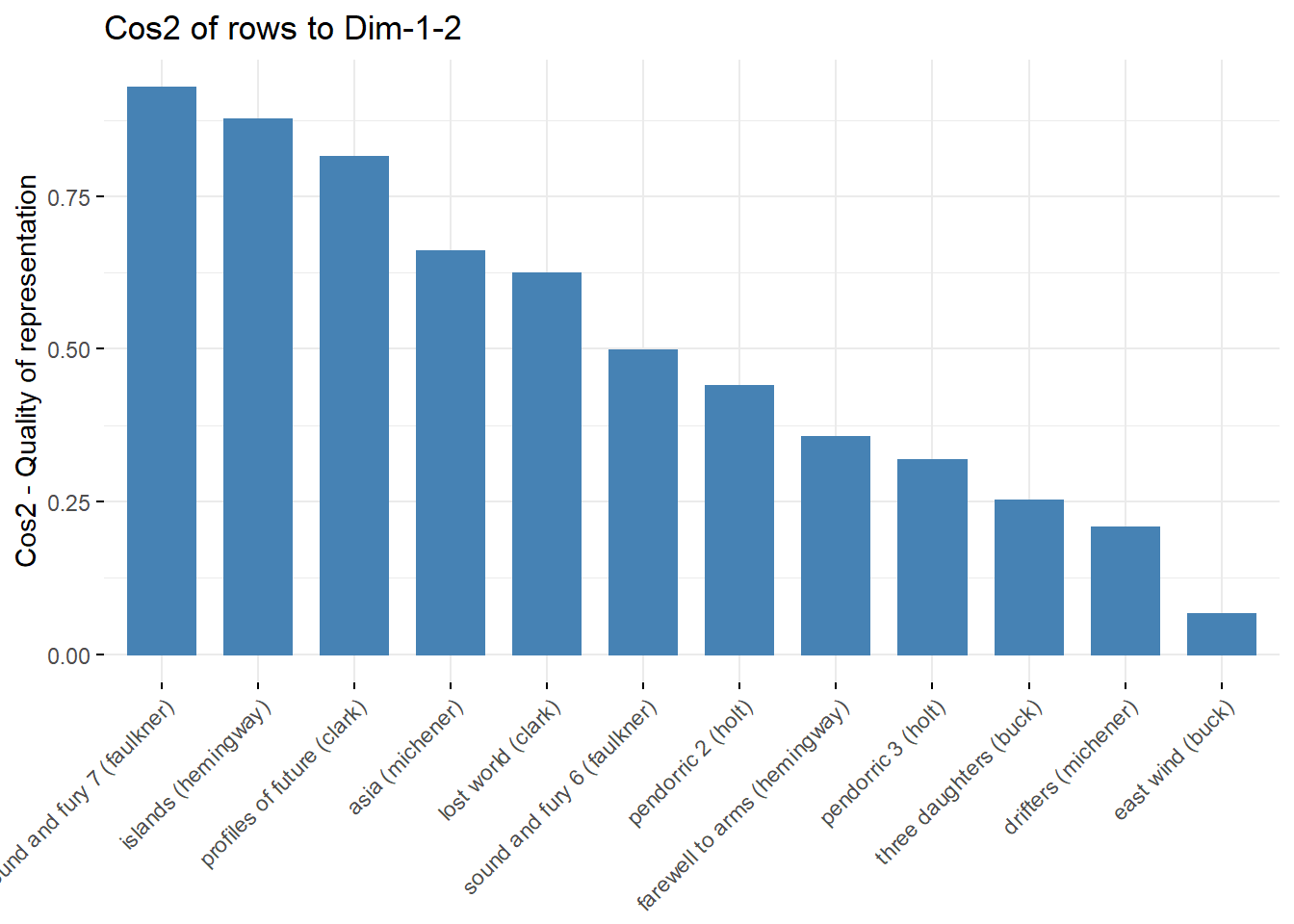
Contribuições de linhas para as dimensões
A contribuição das linhas (em%) para a definição das dimensões pode ser extraída da seguinte forma:
head(row$contrib)
## Dim 1 Dim 2 Dim 3 Dim 4
## three daughters (buck) 0.07770951 5.397889536 9.0348645 3.5769867
## drifters (michener) 1.31224289 1.311355730 6.9016824 3.2091191
## lost world (clark) 11.37829682 0.004534671 1.0701887 9.6067507
## east wind (buck) 0.27039557 1.687558588 38.9462974 0.7999584
## farewell to arms (hemingway) 5.68952570 0.153150170 7.3215552 13.3827381
## sound and fury 7 (faulkner) 0.75082630 60.342337137 0.2710708 4.0971142
## Dim 5
## three daughters (buck) 11.02111308
## drifters (michener) 0.05742143
## lost world (clark) 15.21394286
## east wind (buck) 8.25402749
## farewell to arms (hemingway) 10.25250852
## sound and fury 7 (faulkner) 0.76536675As variáveis de linha com o valor maior contribuem mais para a definição das dimensões.
As linhas que mais contribuem para Dim.1 e Dim.2 são as mais importantes para explicar a variabilidade no conjunto de dados.
Linhas que não contribuem muito para nenhuma dimensão ou que contribuem para as últimas dimensões são menos importantes.É possível usar a função corrplot() para destacar os pontos de linha que mais contribuem para cada dimensão:
corrplot(row$contrib, is.corr=FALSE)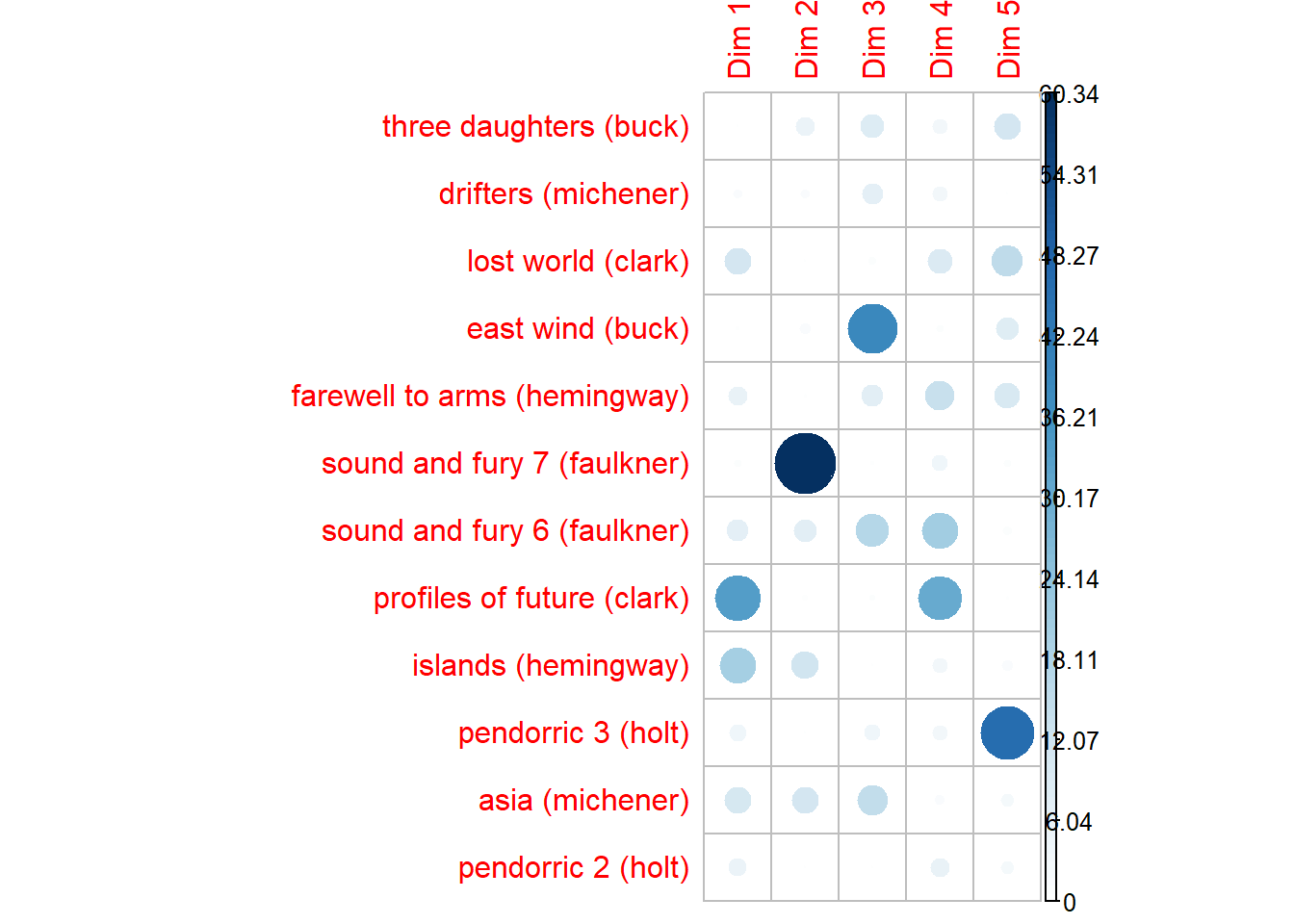 
A função fviz_contrib() pode ser usada para desenhar um gráfico de barras de contribuições de linha. Se seus dados contiverem muitas linhas, você pode optar por mostrar apenas as principais linhas que contribuem:
# Contributions of rows to dimension 1
fviz_contrib(ca3, choice = "row", axes = 1, top = 10)
# Contributions of rows to dimension 2
fviz_contrib(ca3, choice = "row", axes = 2, top = 10)Attaching package: ‘gridExtra’
The following object is masked from ‘package:dplyr’:
combine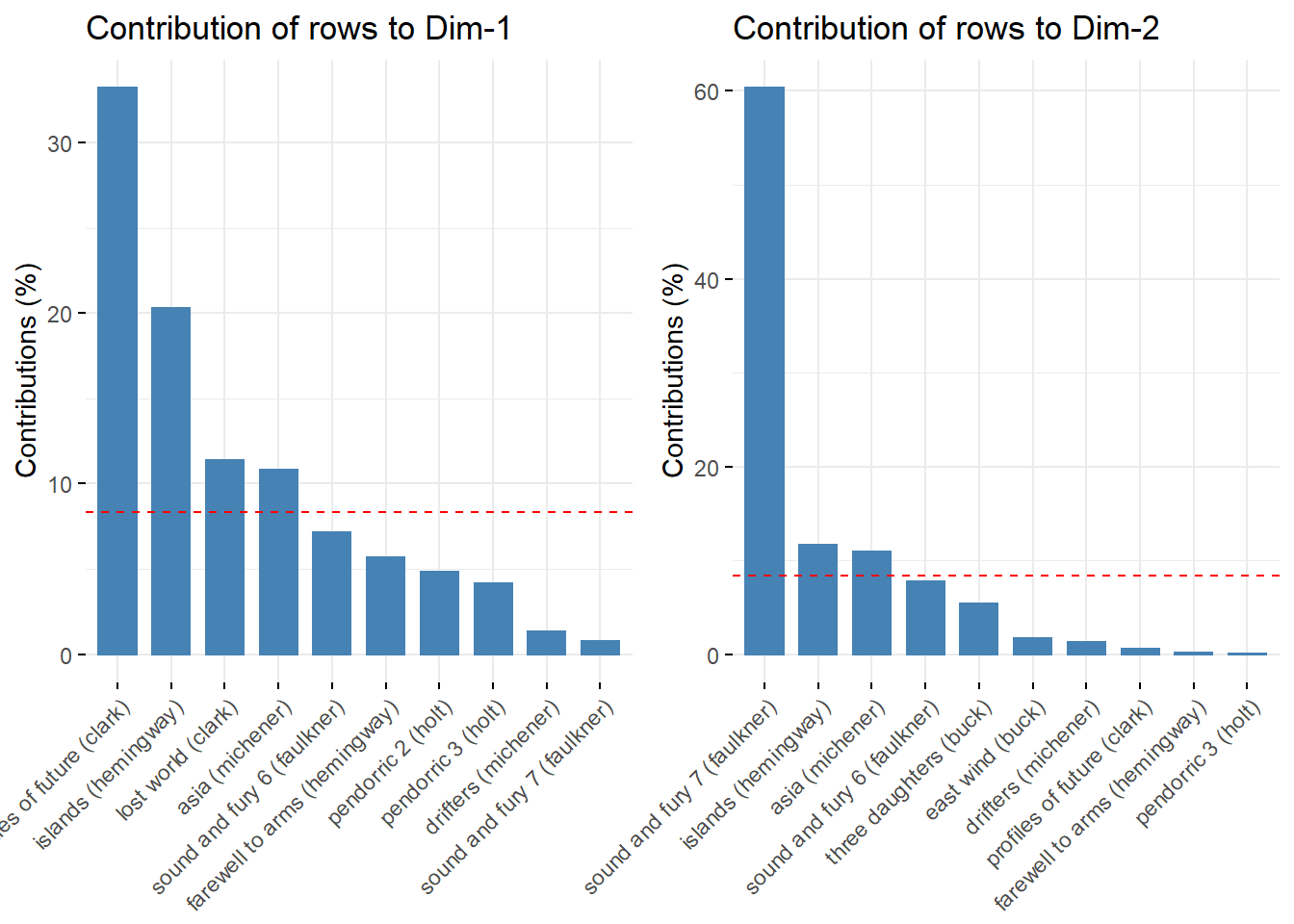
Pode ser visto que William Faulkner e o Hemingway são os que mais contribuem para a dimensão 2.
fviz_ca_row(ca3, col.row = "contrib",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE)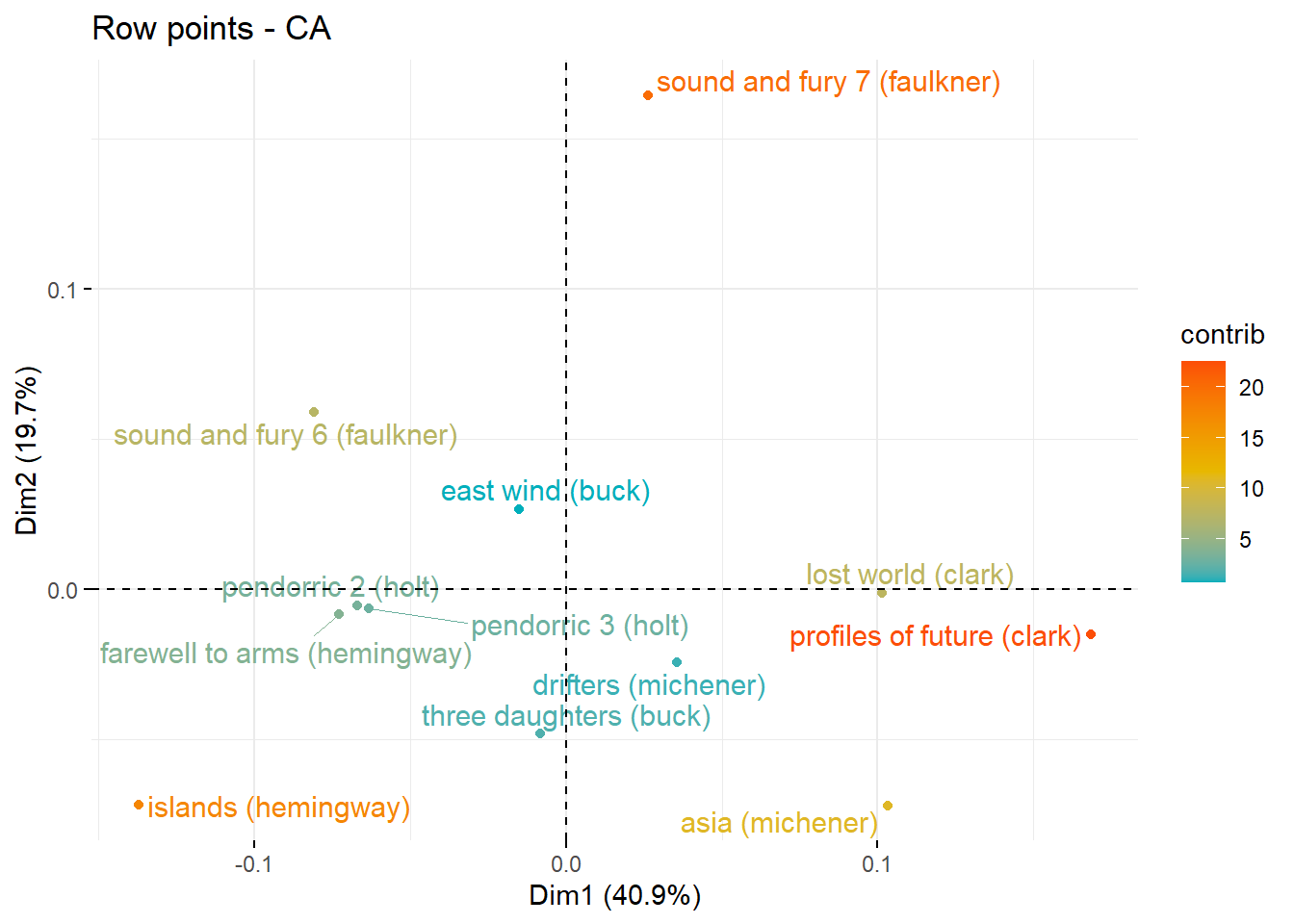
O gráfico de dispersão fornece uma idéia de para qual pólo das dimensões as categorias de linha estão realmente contribuindo.
Por exemplo, a dimensão 2 é definida principalmente pela oposição ao Hemingway (polo negativo) e pelo Faulkner (polo positivo).
Gráfico de variáveis de colunas
A função get_ca_col() é usada para extrair os resultados para variáveis de coluna. Esta função retorna uma lista contendo as variáveis de coordenadas e cos2() (the squared cosine) das colunas:
col <- get_ca_col(ca3)
col
## Correspondence Analysis - Results for columns
## ===================================================
## Name Description
## 1 "$coord" "Coordinates for the columns"
## 2 "$cos2" "Cos2 for the columns"
## 3 "$contrib" "contributions of the columns"
## 4 "$inertia" "Inertia of the columns"
# Coordinates of column points
head(col$coord)
## Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
## a 0.001542787 -0.01945057 0.01327806 -0.02408824 0.014040445
## b 0.086183340 -0.02417310 -0.05642131 0.06025018 0.012791777
## c 0.185156960 -0.08341168 0.05553300 0.03547341 0.034391884
## d -0.168576481 -0.06895233 -0.01440512 0.00888620 0.005075891
## e 0.007591921 -0.04158806 -0.04929204 -0.01359512 0.004840620
## f 0.111751535 -0.04451333 0.01898018 0.01639602 -0.049298987
# Quality of representation
head(col$cos2)
## Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
## a 0.00101434 0.16122650 0.075134803 0.247275878 0.0840104680
## b 0.33844582 0.02662607 0.145053719 0.165409048 0.0074559717
## c 0.69074434 0.14018161 0.062135450 0.025353804 0.0238313801
## d 0.78771817 0.13178766 0.005751891 0.002188815 0.0007141697
## e 0.01150240 0.34516139 0.484884805 0.036885124 0.0046761330
## f 0.45626270 0.07239159 0.013161594 0.009821659 0.0887940717
# Contributions
head(col$contrib)
## Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
## a 0.002479849 0.8190244 0.5838444 3.3504221 1.5714583
## b 1.520136212 0.2484958 2.0707914 4.1174519 0.2562272
## c 10.198418003 4.3005607 2.9158761 2.0746008 2.6921068
## d 17.044817011 5.9253607 0.3955909 0.2624862 0.1182362
## e 0.095564773 5.9586834 12.8044888 1.6983872 0.2972515
## f 3.167594402 1.0442904 0.2904272 0.3778987 4.7165689
fviz_ca_col(ca3, col.col = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE)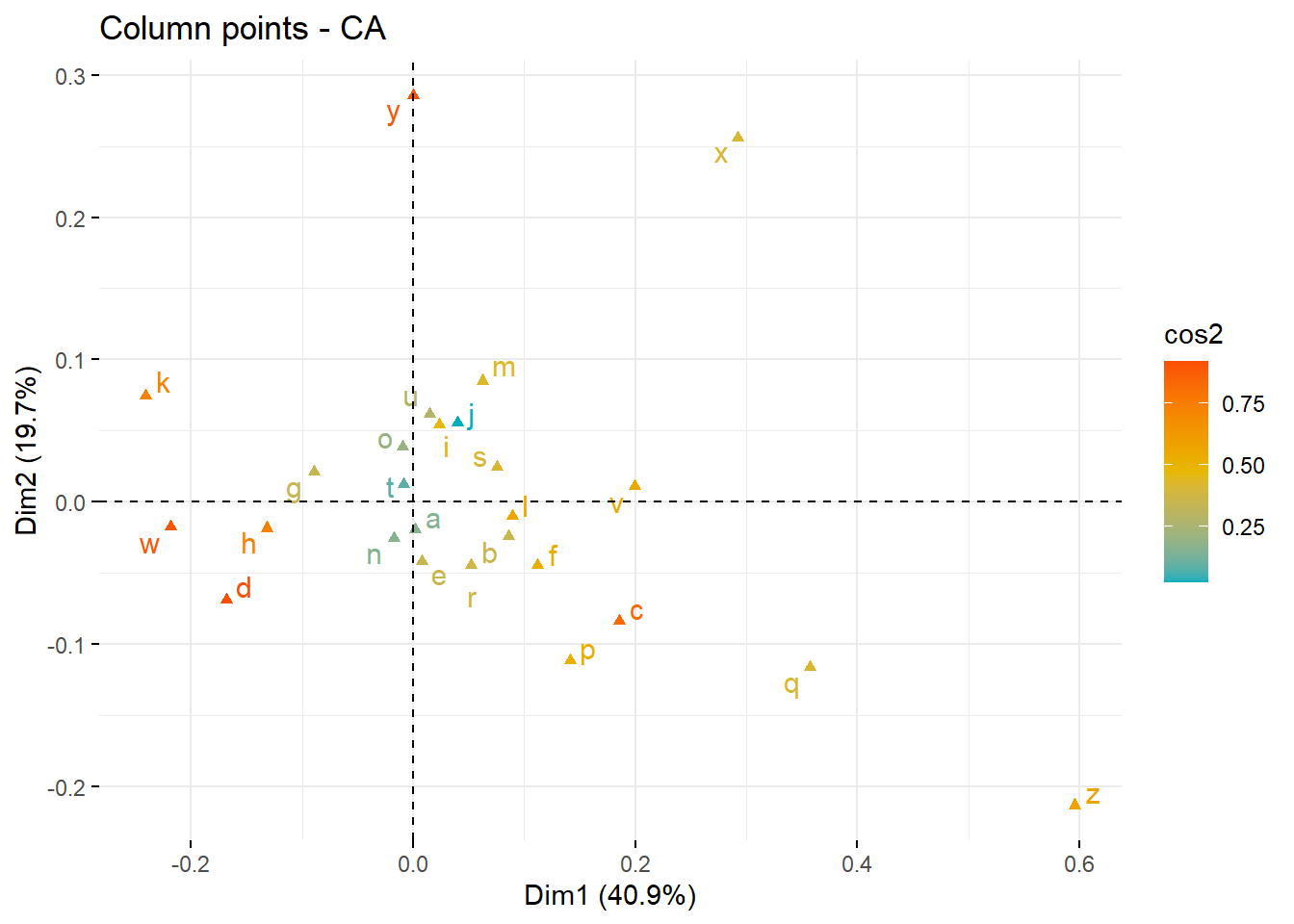
fviz_cos2(ca3, choice = "col", axes = 1:2)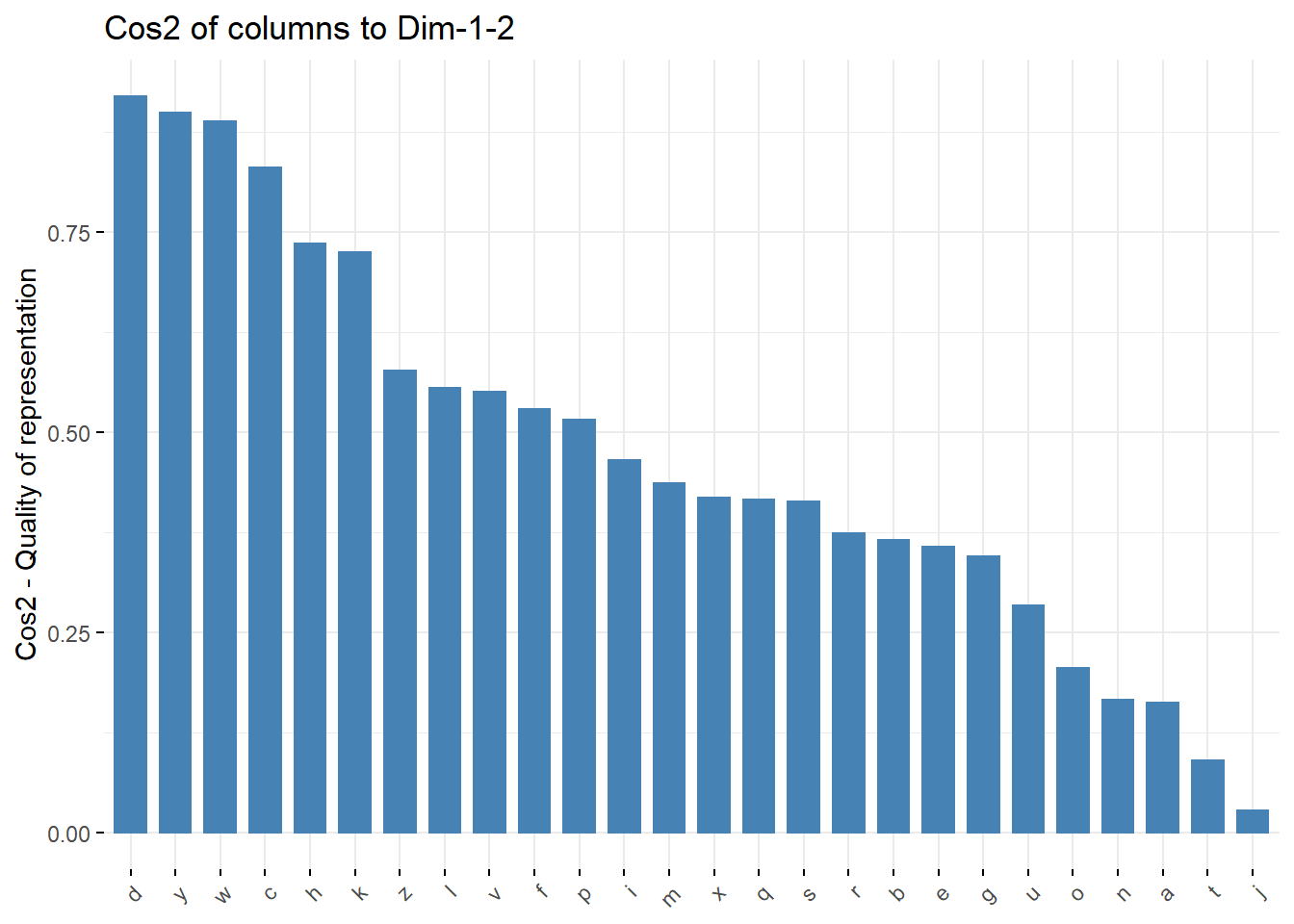
Se você usar o código ou as informações deste guia em um trabalho publicado, solicito que cite-o como uma fonte nas referências bibliográficas.
DUTT-ROSS,Steven Introdução à Análise de Correspondência. Rio de Janeiro. 2020. mimeo. Disponível em: https://blog.metodosquantitativos.com/AF_variaveis_nominais/
Outras referências desse texto.
1. https://www.gastonsanchez.com/visually-enforced/how-to/2012/07/19/Correspondence-Analysis/
2. http://www.sthda.com/english/articles/31-principal-component-methods-in-r-practical-guide/113-ca-correspondence-analysis-in-r-essentials/
Para saber sobre outras funções no R e no Python, você pode acessar o meu blog https://blog.metodosquantitativos.com/ ou o meu site pessoal https://steven.metodosquantitativos.com/