Introdução à Análise de Fatorial - Interpretação
Análise fatorial
Multivariada
Interpretação
Introdução
Você não precisa usar o R… pode usar o Python também.
Análise Fatorial
Essa é a parte 2 da Análise Fatorial com a interpretação. A parte 1 contendo a discussão de pressuposto e a decisão sobre o número de fatores pode ser encontrada aqui. https://metodos.netlify.app/docs/af_continuas/
Exemplo: o ansiedade.RData (questionário de ansiedade com a linguagem R) Vamos prosseguir com nosso exemplo hipotético da pesquisa com o Questionário de Ansiedade com a linguagem R.
O banco de dados consiste nas seguintes questões:
- Estatísticas me fazem chorar
- Meus amigos vão pensar que sou estúpido por não ser capaz de lidar com R
- Adoro Desvios padrão
- Eu sonho que Pearson está me atacando com coeficientes de correlação
- Eu não entendo estatística
- Eu tenho pouca experiência com computadores
- Todos os computadores me odeiam
- Eu nunca fui bom em matemática
Vamos começar carregando a base de dados no R e construindo uma matriz de correlação de Pearson.
load(url("https://github.com/DATAUNIRIO/Base_de_dados/raw/master/ansiedade.RData"))
ls()[1] "ansiedade" "dicionario"library(corrplot)
correlacao<-cor(ansiedade)
corrplot.mixed(correlacao)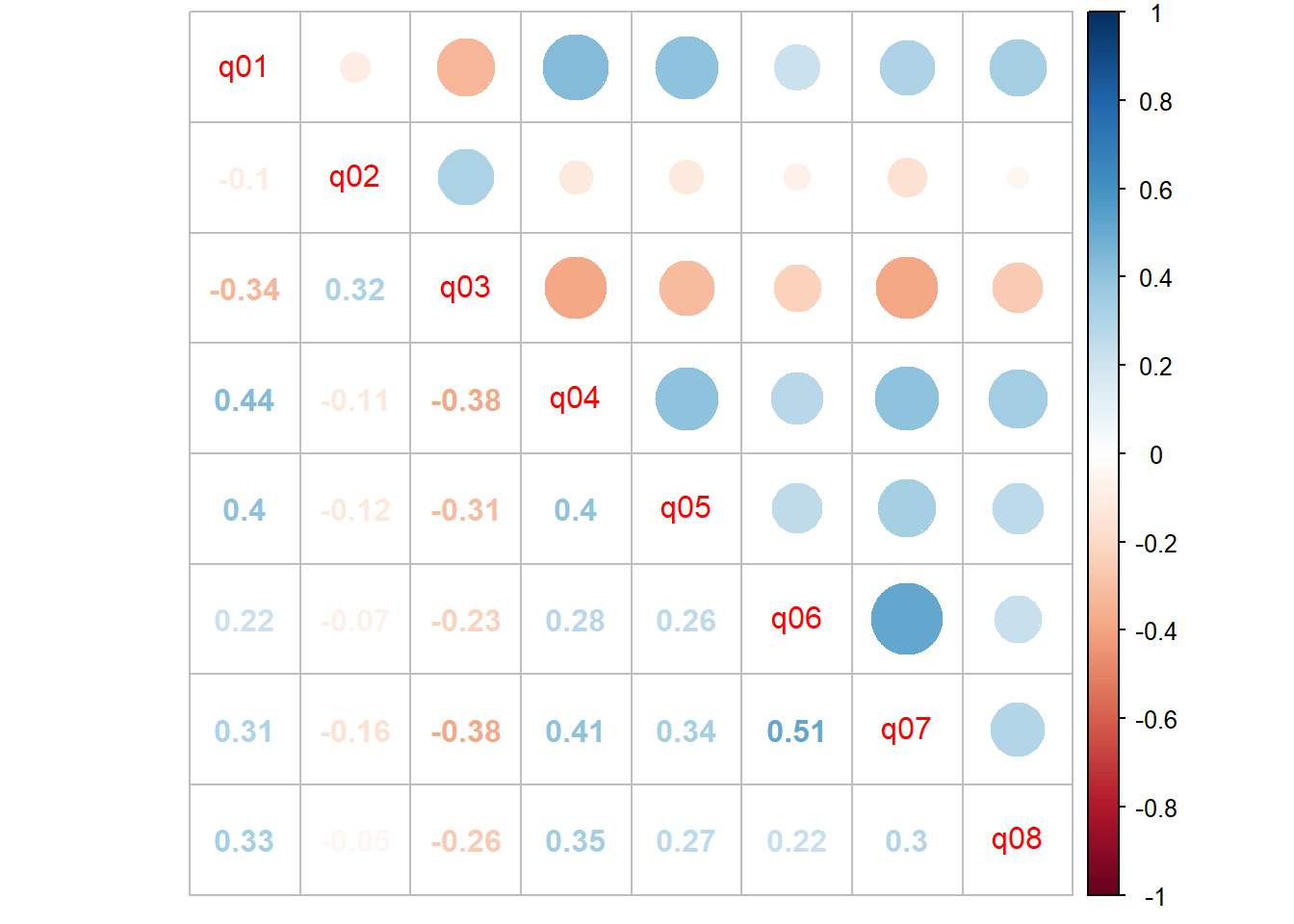
Executando Análise Fatorial
library(psych)
analise_fatorial <- fa(correlacao, nfactors=2, rotate="varimax")
#
analise_fatorial[["communalities"]] q01 q02 q03 q04 q05 q06 q07
0.43392342 0.05187725 0.31920090 0.46074127 0.34486315 0.29452262 0.91175953
q08
0.23618496 # Cargas fatoriais (factor loadings)
analise_fatorial[["loadings"]]
Loadings:
MR1 MR2
q01 0.643 0.141
q02 -0.190 -0.126
q03 -0.492 -0.277
q04 0.625 0.265
q05 0.545 0.218
q06 0.237 0.488
q07 0.263 0.918
q08 0.443 0.200
MR1 MR2
SS loadings 1.702 1.351
Proportion Var 0.213 0.169
Cumulative Var 0.213 0.382# PCA Variable Factor Map
library(FactoMineR)
resultado <- PCA(ansiedade) # graphs generated automatically 
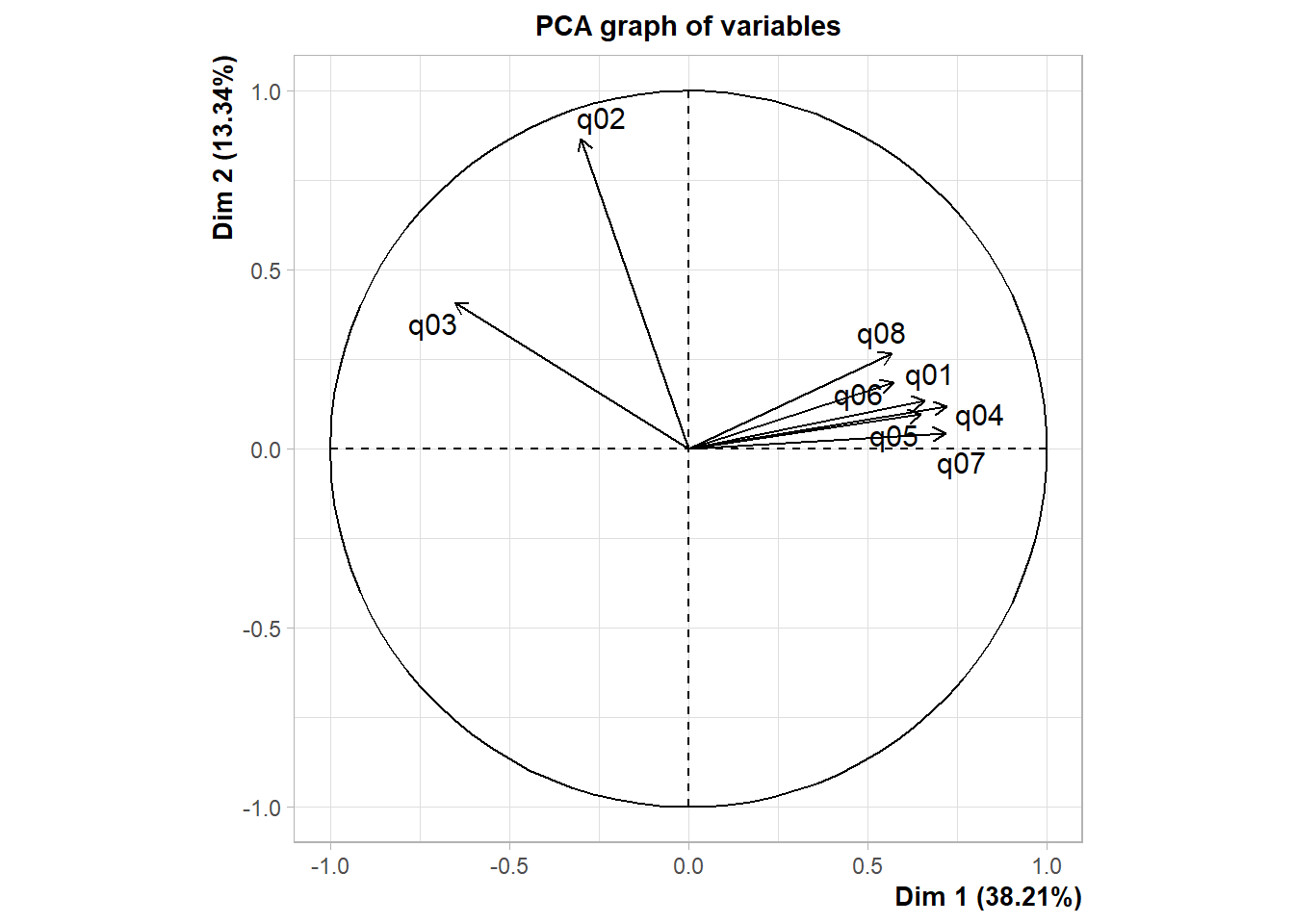
Olhando o mapa de variáveis criado a partir do comando PCA do pacote FactoMineR, podemos ver que dois grupos.
Interpretação
As cargas fatoriais (factor loadings) indicam o quanto um fator explica uma variável. As cargas podem variar de -1 a 1.
Examine o padrão de carregamento para determinar o fator que tem maior influência em cada variável. Cargas próximas a -1 ou 1 indicam que o fator influencia fortemente a variável. Cargas próximas a 0 indicam que o fator tem uma influência fraca na variável. Algumas variáveis podem ter cargas elevadas em vários fatores.
Cargas fatoriais são a correlação de cada variável com o fator. Cargas indicam o grau de correspondência entre a variável e o fator, com cargas maiores tornando a variável representativa do fator. Cargas fatoriais são o meio de interpretar o papel que cada variável tem na definição de cada fator (Hair et al, 2006).
No nosso caso, a q02 (“Meus amigos vão pensar que sou estúpido por não ser capaz de lidar com R”) parece não estar relacionado com nenum fator.
Hair et al (2006) e Figueiredo Filho & Silva Junior,(2010) sugerem que um dos pressupostos da análise fatorial é a estrutura simples de seus componentes. O argumento defende que a mesma variável não pode contribuir para a construção de fatores distintos. Adota-se 0,40 como limite aceitável da contribuição da variável na criação do fator com o objetivo de evitar o problema da indeterminação da relação entre variáveis e fatores. Uma boa ideia seria eliminar a q02 da análise fatorial.
Cumpre registrar que o % Variabilidade Explicada é muito baixo.Apenas 0,382.
dados<-tibble::tribble(~q,~ROTULO, ~MR1, ~MR2,
"q01","1.Estatísticas me fazem chorar", "0.643", "0.141",
"q02", "2.Meus amigos vão pensar que sou estúpido por não ser capaz de lidar com R", "-0.19", "-0.126",
"q03","3.Adoro Desvios padrão", "-0.492", "-0.277",
"q04","4.Eu sonho que Pearson está me atacando com coeficientes de correlação", "0.625", "0.265",
"q05","5.Eu não entendo estatística", "0.545", "0.218",
"q06","6.Eu tenho pouca experiência com computadores", "0.237", "0.488",
"q07","7.Todos os computadores me odeiam", "0.263", "0.918",
"q08","8.Eu nunca fui bom em matemática", "0.443", "0.2"
)
library(formattable)
improvement_formatter <- formatter("span",
style = x ~ style(font.weight = "bold",
color = ifelse(x > 0.4, "blue",
ifelse(x == -0.492, "red",
ifelse(x > -0.2, "black", "black")))),
x ~ icontext(ifelse(x>0, "arrow-up", "arrow-down"), x))
formattable(dados, align =c("l","l","r","r"), list(
`ROTULO` = formatter("span", style = ~ style(color = "black",font.weight = "bold")),
`MR1`= improvement_formatter,
`MR2`= improvement_formatter))| q | ROTULO | MR1 | MR2 |
|---|---|---|---|
| q01 | 1.Estatísticas me fazem chorar | 0.643 | 0.141 |
| q02 | 2.Meus amigos vão pensar que sou estúpido por não ser capaz de lidar com R | -0.19 | -0.126 |
| q03 | 3.Adoro Desvios padrão | -0.492 | -0.277 |
| q04 | 4.Eu sonho que Pearson está me atacando com coeficientes de correlação | 0.625 | 0.265 |
| q05 | 5.Eu não entendo estatística | 0.545 | 0.218 |
| q06 | 6.Eu tenho pouca experiência com computadores | 0.237 | 0.488 |
| q07 | 7.Todos os computadores me odeiam | 0.263 | 0.918 |
| q08 | 8.Eu nunca fui bom em matemática | 0.443 | 0.2 |
Rótulo dos fatores:
Considerando as cargas fatorias, podemos rotular os fatores:
- Ansiedade Matemática/EStatística
- Ansiedade com computadores
dados<-tibble::tribble(~FATOR,~q,~ROTULO, ~MR1, ~MR2,
"Fator 1","q01","1.Estatísticas me fazem chorar", "0.643", "0.141",
"Fator 1","q03","3.Adoro Desvios padrão", "-0.492", "-0.277",
"Fator 1","q04","4.Eu sonho que Pearson está me atacando com coeficientes de correlação", "0.625", "0.265",
"Fator 1","q05","5.Eu não entendo estatística", "0.545", "0.218",
"Fator 1","q08","8.Eu nunca fui bom em matemática", "0.443", "0.2",
"Fator 2","q06","6.Eu tenho pouca experiência com computadores", "0.237", "0.488",
"Fator 2","q07","7.Todos os computadores me odeiam", "0.263", "0.918"
)
improvement_formatter <- formatter("span",
style = x ~ style(font.weight = "bold",
color = ifelse(x > 0.4, "blue",
ifelse(x == -0.492, "red",
ifelse(x > -0.2, "black", "black")))) )
formattable(dados, align =c("l","l","r","r"), list(
`FATOR` = formatter("span", style = ~ style(color = "black",font.weight = "bold")),
`MR1`= improvement_formatter,
`MR2`= improvement_formatter))| FATOR | q | ROTULO | MR1 | MR2 |
|---|---|---|---|---|
| Fator 1 | q01 | 1.Estatísticas me fazem chorar | 0.643 | 0.141 |
| Fator 1 | q03 | 3.Adoro Desvios padrão | -0.492 | -0.277 |
| Fator 1 | q04 | 4.Eu sonho que Pearson está me atacando com coeficientes de correlação | 0.625 | 0.265 |
| Fator 1 | q05 | 5.Eu não entendo estatística | 0.545 | 0.218 |
| Fator 1 | q08 | 8.Eu nunca fui bom em matemática | 0.443 | 0.2 |
| Fator 2 | q06 | 6.Eu tenho pouca experiência com computadores | 0.237 | 0.488 |
| Fator 2 | q07 | 7.Todos os computadores me odeiam | 0.263 | 0.918 |
Bibliografia
- FIGUEIREDO FILHO, Dalson Brito; SILVA JUNIOR, José Alexandre da. Visão além do alcance: uma introdução à análise fatorial. Opin. Publica, Campinas , v. 16, n. 1, p. 160-185, June 2010 . Available from http://www.scielo.br/scielo.php?script=sci_arttext&pid=S0104-62762010000100007&lng=en&nrm=iso. access on 06 Sept. 2020. https://doi.org/10.1590/S0104-62762010000100007.
- HAIR, Jr; BLACK, W. C; BABIN, B. J; ANDERSON, R. E e TATHAM, R. L. Multivariate Data Analysis. 6ª edição. Upper Saddle River, NJ: Pearson Prentice Hall, 2006.
______________3 Análise Fatorial.[https://www.maxwell.vrac.puc-rio.br/8741/8741_5.PDF](https://www.maxwell.vrac.puc-rio.br/8741/8741_5.PDF)
