Introdução à Análise de Fatorial
Análise fatorial
Multivariada
Introdução
Você não precisa usar o R… pode usar o Python também.
Análise Fatorial
Essa é uma tradução. O original pode ser encontrado aqui. https://stats.idre.ucla.edu/spss/seminars/introduction-to-factor-analysis/a-practical-introduction-to-factor-analysis/
Análise Fatorial Exploratória
Introdução
Suponha que você esteja conduzindo uma pesquisa e queira saber se os itens da pesquisa têm padrões de respostas semelhantes. Esses itens “se encaixam” para criar uma conceito?
O pressuposto básico da análise fatorial é que, para uma coleção de variáveis observadas, existe um conjunto de variáveis subjacentes chamadas fatores (menores do que as variáveis observadas), que podem explicar as inter-relações entre essas variáveis. Digamos que você conduza uma pesquisa e colete respostas sobre a ansiedade das pessoas sobre o uso do R. Todos esses itens realmente medem o que chamamos de “ansiedade com a linguagem R”?

ansiedade com a linguagem R
Exemplo: o ansiedade.RData (questionário de ansiedade com a linguagem R) Vamos prosseguir com nosso exemplo hipotético da pesquisa com o Questionário de Ansiedade com a linguagem R.
O banco de dados consiste nas seguintes questões:
- Estatísticas me fazem chorar
- Meus amigos vão pensar que sou estúpido por não ser capaz de lidar com R
- Adoro Desvios padrão
- Eu sonho que Pearson está me atacando com coeficientes de correlação
- Eu não entendo estatística
- Eu tenho pouca experiência com computadores
- Todos os computadores me odeiam
- Eu nunca fui bom em matemática
Vamos começar carregando a base de dados no R e construindo uma matriz de correlação de Pearson.
load(url("https://github.com/DATAUNIRIO/Base_de_dados/raw/master/ansiedade.RData"))
ls()[1] "ansiedade" "dicionario"Para reproduzir a atividade sobre análise fatorial no R, vou utilizar a mesma base de dados com uma escala de likert.
Todavia, NÃO recomendo utilizar a análise fatorial para escalas de likert. A minha análise das falhas no uso da análise fatorial para escalas de likert pode ser vista aqui https://metodos.netlify.app/docs/af_ordinal/
Também vou deixar ao final uma sugestão de bibliografia para a discussão do uso da escalas de likert com análise fatorial.
library(corrplot)
correlacao<-cor(ansiedade)
corrplot.mixed(correlacao)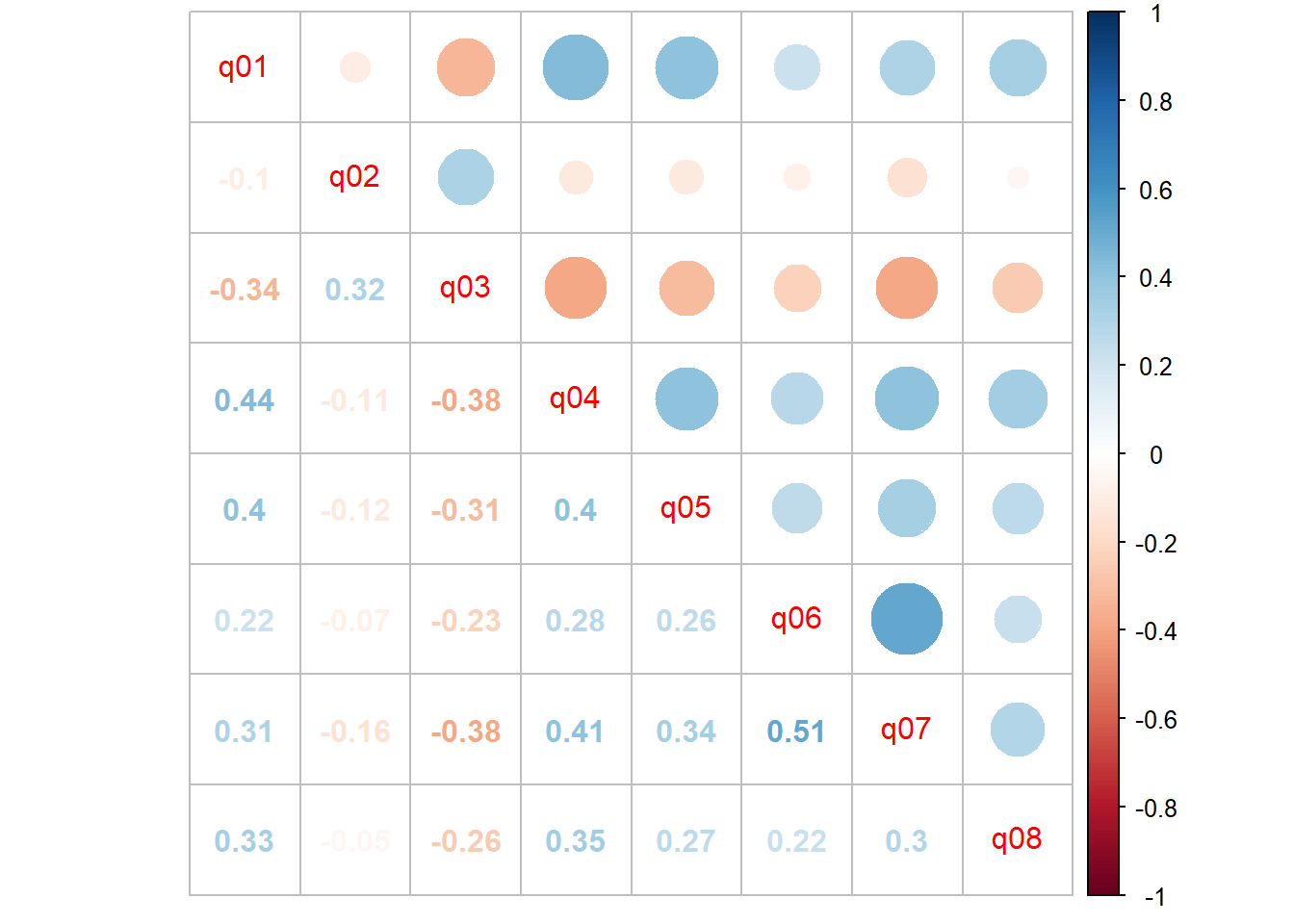
A partir da matriz de correlação, podemos ver que a maioria dos itens tem alguma correlação entre si, variando de rho = −0,38 para os itens 3 e 7 a rho = 0,51 para os itens 6 e 7. Devido às correlações altas entre os itens, é uma boa estratégia tentar aplicar à análise fatorial nessa base de dados.
Lembre-se de que o objetivo da análise fatorial é modelar as inter-relações entre itens com menos variáveis (latentes). Essas inter-relações podem ser divididas em vários componentes. Vou apresenta-los a seguir:
Particionando a variância em uma análise fatorial
Uma vez que o objetivo da análise fatorial é modelar as inter-relações entre os itens, nos concentramos principalmente na variância e covariância, e não na média. A análise fatorial assume que a variância pode ser dividida em dois tipos de variância, comum e única.
A variância comum é a quantidade de variação que é compartilhada entre um conjunto de itens. Os itens altamente correlacionados compartilharão muita variância. Comunalidade é uma definição de variância comum que varia entre 0 e 1. Valores mais próximos de 1 sugerem que os fatores extraídos explicam mais da variância de um item individual.
Variância única é qualquer porção de variação que não seja comum. Existem dois tipos: Variância específica: é a variância que é específica para um determinado item (por exemplo, o Item 4 “Todos os computadores me odeiam” pode ter uma variação que é atribuível à ansiedade sobre os computadores, além da ansiedade sobre R). Variância do erro: vem de erros de medição e basicamente qualquer coisa inexplicada pela variação comum ou específica (por exemplo, a pessoa recebeu uma ligação de sua babá informando que seu filho de dois anos comeu seu batom favorito).
A figura abaixo mostra como esses conceitos estão relacionados:

A variância total é composta pela variância comum e pela variância única, e a variância única é composta pela variância específica e pelo erro aleatório (obs- erro aleatório é diferente de erro sistemático). Se a variância total for 1, então a comunalidade é h2 e a variância única é 1 − h2. Vamos dar uma olhada em como a partição de variância se aplica ao modelo de análise fatorial.

Aqui você vê que a ansiedade com a linguagem R compõe a variância comum para todos os oito itens, mas dentro de cada item há variância específica e variância de erro. Veja o exemplo do item 7 “Os computadores são úteis apenas para jogar”. Embora a ansiedade com a linguagem R explique parte dessa variação, pode haver fatores sistemáticos, como tecnofobia e fatores não sistêmicos que não podem ser explicados pela ansiedade com a linguagem R ou tecnofbia, como obter uma multa por excesso de velocidade antes de chegar ao centro de pesquisa (erro de medição). Agora que entendemos o particionamento da variância, podemos prosseguir para a realização de nossa primeira análise fatorial. Na verdade, as suposições que fazemos sobre o particionamento de variância afetam as análises que executamos.
Executando Análise Fatorial
Como técnica de análise de dados, o objetivo de uma análise fatorial é reduzir o número de variáveis para explicar e interpretar os resultados. Isso pode ser feito em duas etapas:
- extração de fator
- rotação do fator
A extração de fator envolve fazer uma escolha sobre o tipo de modelo, bem como o número de fatores a serem extraídos. A rotação de fator ocorre depois que os fatores são extraídos, com o objetivo de obter uma estrutura simples a fim de melhorar a interpretabilidade.
Pressupostos
Teste de Esfericidade de Bartlett
O teste de esfericidade de Bartlett avalia a hipótese de que a matriz de correlações pode ser a matriz identidade com determinante igual a 1.
Se a matriz de correlações for igual à matriz identidade, isso significa que não devemos utilizar a análise fatorial. > H0: a matriz de correlações é uma matriz identidade
Kaiser-Meyer-Olkin - KMO
A estatística KMO, cujos valores variam de 0 a 1, avalia a adequação da amostra quanto ao grau de correlação parcial entre os valores, que deve ser pequeno•O valor de KMO próximo de 0 indica que a análise fatorial pode não ser adequada (correlação fraca entre as variáveis)•Quanto mais próximo de 1 o seu valor, mais adequada é a utilização da técnica.
library(REdaS)
# Bartlett's Test of Sphericity
bart_spher(ansiedade) Bartlett's Test of Sphericity
Call: bart_spher(x = ansiedade)
X2 = 4157.283
df = 28
p-value < 2.22e-16# Kaiser-Meyer-Olkin Statistics
KMOS(ansiedade, use = "pairwise.complete.obs")
Kaiser-Meyer-Olkin Statistics
Call: KMOS(x = ansiedade, use = "pairwise.complete.obs")
Measures of Sampling Adequacy (MSA):
q01 q02 q03 q04 q05 q06 q07 q08
0.8386706 0.6762543 0.8178404 0.8480822 0.8686018 0.7534405 0.7801035 0.8817585
KMO-Criterion: 0.8176944Extração de Fatores
Determinando o número de fatores a extrair. A primeira decisão para extrair os fatores é escolher o número de fatores. O pacote nFactors oferece um conjunto de funções para auxiliar nessa decisão. Basicamente, temos três abordagens para decidir a quantidade de fatores.
- Critério da raiz latente (critério de Kaiser): Escolhe-se o número de fatores, em função do número de autovalores (eigenvalues) acima de 1. Os autovalores mostram a variância explicada por cada fator, ou seja, o quanto cada fator explica da variância total.
- Critério do cotovelo no gráfico Screeplot: Utilizado para identificar o número ótimo de fatores que podem ser extraídos antes que o gráfico faça um cotovelo.
- Critério da interpretabilidade: Qualquer solução fatorial deve ser interpretável para ser útil.
# Determine Number of Factors to Extract
library(nFactors)
ev <- eigen(cor(ansiedade)) # get eigenvalues
ap <- parallel(subject=nrow(ansiedade),var=ncol(ansiedade),
rep=100,cent=.05)
nS <- nScree(x=ev$values, aparallel=ap$eigen$qevpea)
plotnScree(nS) 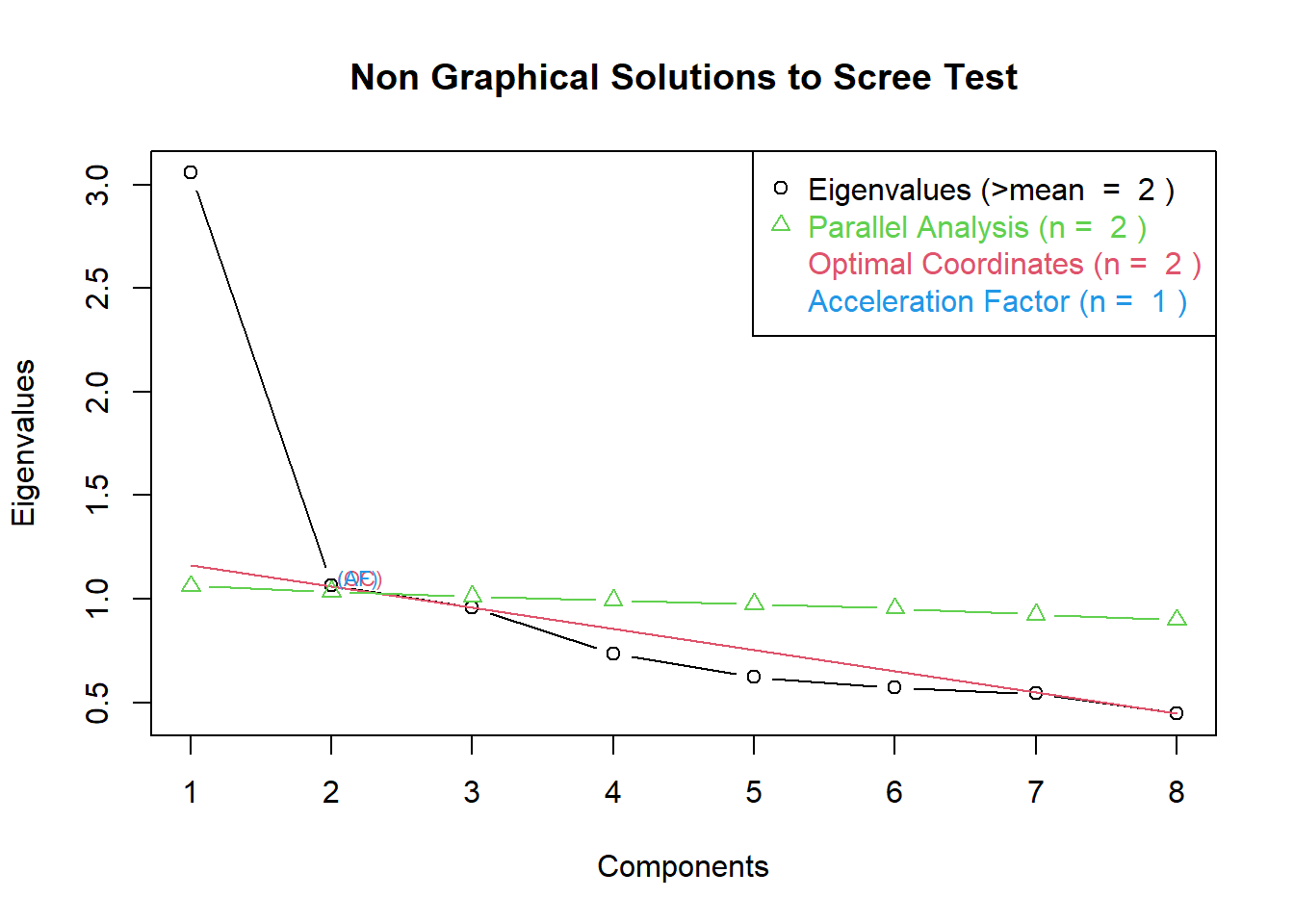
Por meio dos critérios do cotovelo e da raiz latente, acredito que devemos ter dois fatores.
library(psych)
analise_fatorial <- fa(correlacao, nfactors=2, rotate="varimax")
analise_fatorial$loadings
Loadings:
MR1 MR2
q01 0.643 0.141
q02 -0.190 -0.126
q03 -0.492 -0.277
q04 0.625 0.265
q05 0.545 0.218
q06 0.237 0.488
q07 0.263 0.918
q08 0.443 0.200
MR1 MR2
SS loadings 1.702 1.351
Proportion Var 0.213 0.169
Cumulative Var 0.213 0.382Nem sempre os fatores produzidos na fase de extração são facilmente interpretados. O método de rotação tem por objetivo transformar os coeficientes dos componentes principais retidos em uma estrutura simplificada.
A rotação varimax é o método mais popular e visa extremar os valores das cargas fatoriais (loadings), de modo que cada variável se associe a apenas um fator. Variáveis com baixa carga fatorial devem ser eliminadas.
FactoMineR
O pacote FactoMineR oferece um grande número de funções adicionais para a análise fatorial exploratória. Isso inclui o uso de variáveis quantitativas e qualitativas, bem como a inclusão de variáveis suplementares.
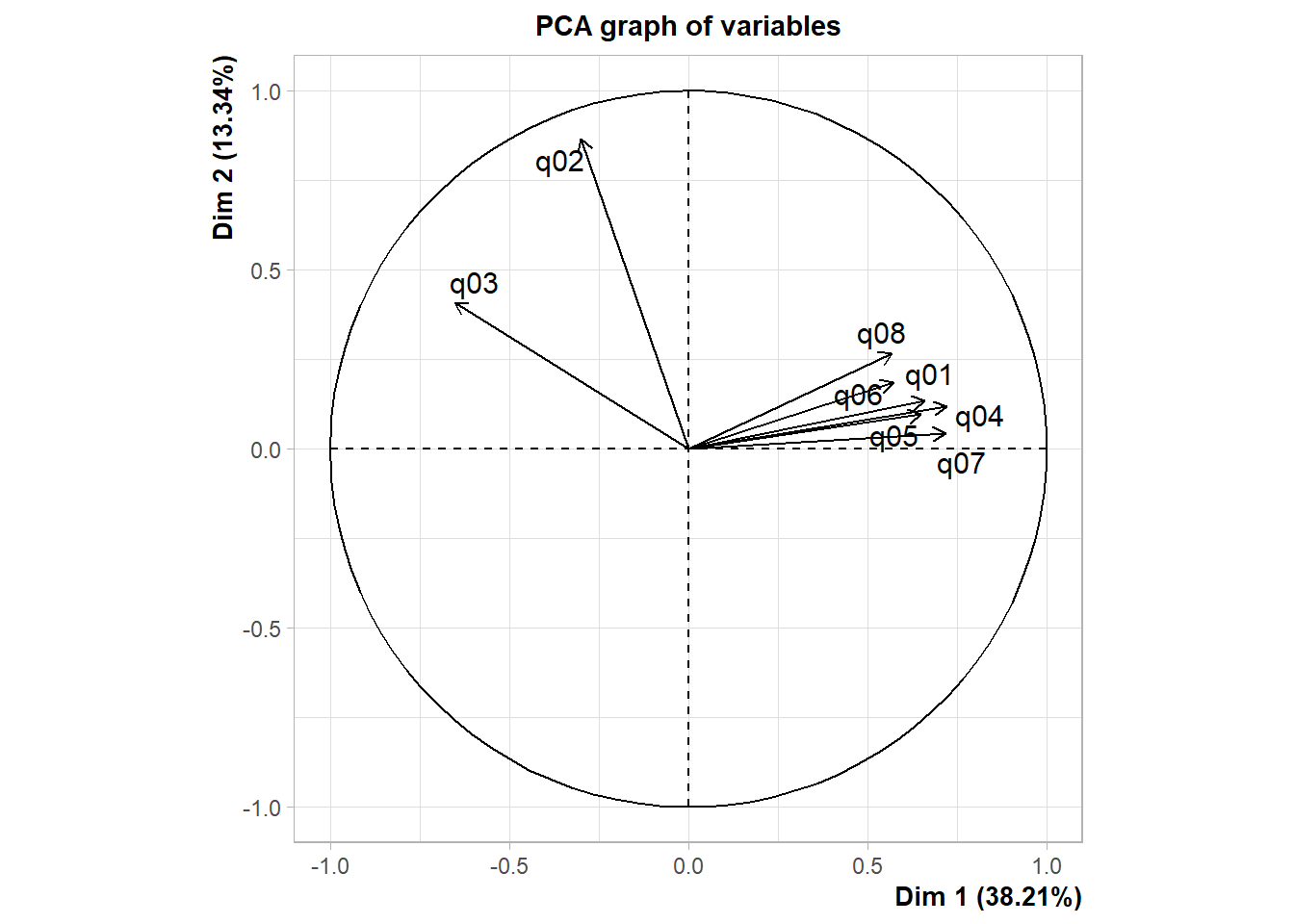
# PCA Variable Factor Map
library(FactoMineR)
resultado <- PCA(ansiedade) # graphs generated automatically 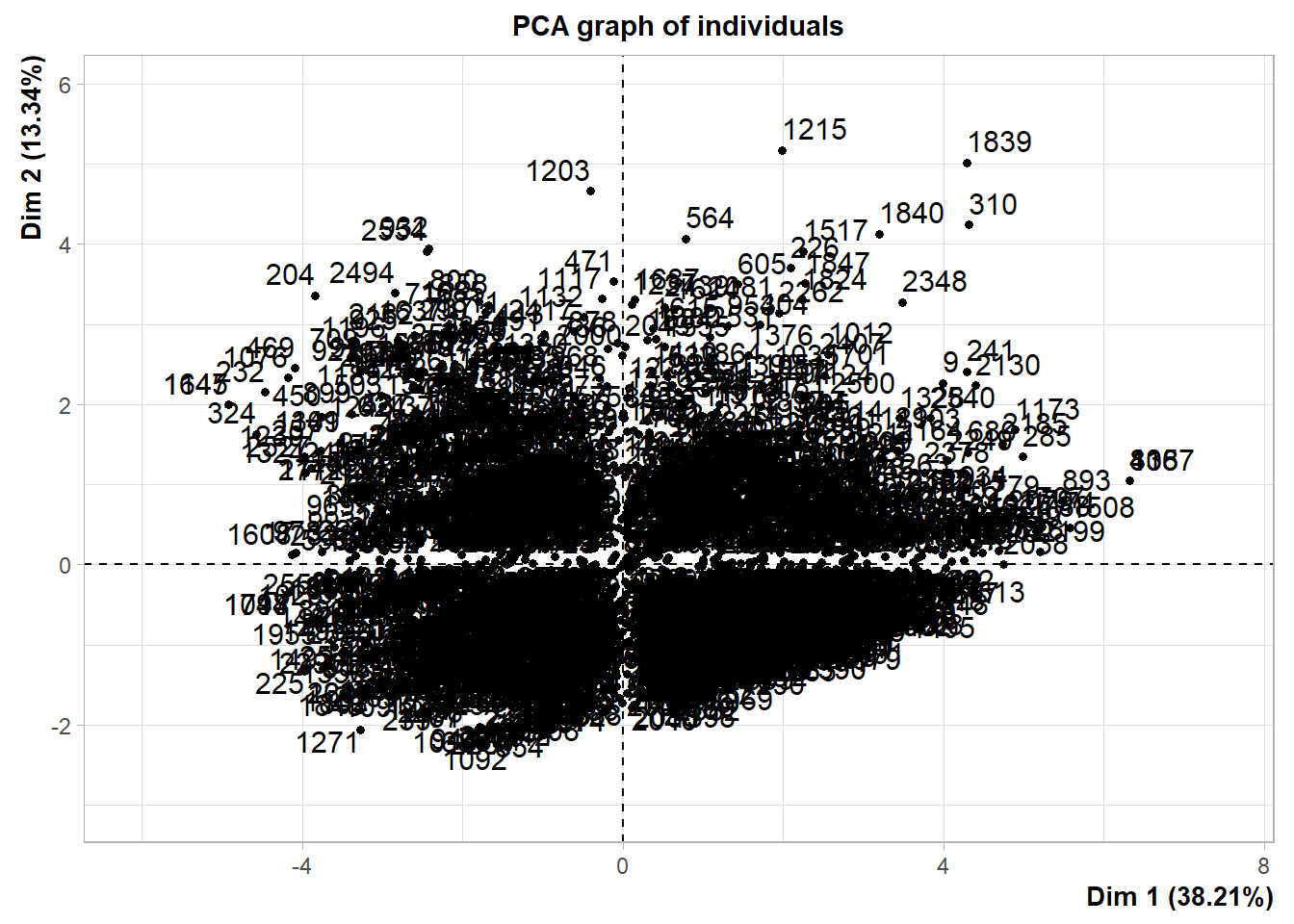
Análise fatorial confirmatória e o modelo de equações estruturais no R
# Simple CFA Model
library(sem)
ansiedade.cov <- cov(ansiedade)
model.ansiedade <- specify.model
ansiedade.sem <- sem(model.ansiedade, ansiedade.cov, nrow(ansiedade))
# print results (fit indices, paramters, hypothesis tests)
summary(ansiedade.sem)
# print standardized coefficients (loadings)
std.coef(ansiedade.sem) Você pode usar a função boot.sem() para fazer o bootstrap do modelo de equações estruturais. Sugiro que você dê uma olhada no pacote lavaan do R.
Análise fatorial não linear
Essa é uma tradução. O original pode ser encontrado aqui. https://alice86.github.io/2018/04/08/Factor-Analysis-on-Ordinal-Data-example-in-R-(psych,-homals)/
A Abordagem da análise fatorial não linear
Conforme apresentado antes, o objetivo da análise fatorial é maximizar a proporção de variância dos dados originais explicada por um número limitado de fatores latentes, enquanto com dados ordinais pretendemos encontrar e fixar as distâncias entre as escalas. Na análise fatorial não linear, a técnica chamada optimal scaling é usada para atingir esses dois objetivos ao mesmo tempo, ou digamos, para encontrar uma quantificação categórica de modo que a correlação seja maximizada o máximo possível.
O pressuposto da análise fatorial não linear: As transformações das variáveis podem ser encontradas de forma que todas as regressões bivariadas sejam exatamente lineares (De Leeuw, 2005).
Esta é uma suposição mais fraca do que assumir normalidade multivariada (De Leeuw, 1988) como acontece com a abordagem policórica. Uma limitação desse método é que a restrição de classificação (o número de fatores) deve ser determinada com antecedência, e tal escolha pode ser difícil de justificar porque o critério da variância cumulativa explicada não se aplica.
Análise fatorial não linear no R - disclaimer
Jiayu Wu (2018) utiliza o pacote de homals (Homogeneity analysis) para realizar uma análise fatorial não linear. Todavia, olhando a documentação do pacote homals podemos ver algo do tipo:
This function performs a homogeneity analysis, aka a multiple correspondence analysis.
Sugiro cuidado na aplicação deste método.
Análise fatorial não linear no R - aplicação
Na análise fatorial não linear, a quantificação da categoria é realizada ao mesmo tempo em que maximiza a variância, de modo que as proporções da variância explicada (normalmente medida com autovalores no método clássico) mudam com as restrições de classificação, tornando necessário e difícil determinar antecipadamente o número de fatores.
library(homals)
load("data.RData")
features = dat[1:10]
# nonlinear FA with 3 factors
nfa1 = homals(features, ndim = 3, level = "ordinal")
# nfa1$eigenvalues
nfa0 = homals(features, ndim = 10, level = "ordinal")
# nfa0$eigenvalues
# Screep plots
par(mfrow = c(1,2))
plot(nfa1, plot.type = "screeplot")
plot(nfa0, plot.type = "screeplot")
load("data.RData")
load("nonlinearFA")
# Derive loading matrix
cache = apply(features, 2, function(x) nlevels(as.factor(x)))
ld = unlist(lapply(nfa$loadings, function(x) x[1,]))
loadings = matrix(ld, byrow = T, nrow = 10)
rownames(loadings) = names(cache)
scores = nfa$objscores
x = list()
x$scores <- scores
x$loadings <- loadings
class(x) <- c('psych','fa')
# Biplot by Gender
biplot(x, pch=c(21,16)[dat[,"Gender"]+1],
group = (dat[,"Gender"]+1),
xlim.s=c(-0.035,0.035),ylim.s=c(-0.02,0.035), arrow.len = 0.1,
main="Biplot with observations by gender",
col = c("orange","blue"), pos = 3)
# Loading plot
plot(nfa, plot.type = "loadplot", asp = 1)Referências
- Jamieson, Susan. “Likert scales: How to (ab) use them?.” Medical education 38.12 (2004): 1217-1218.
- Knapp TR. Treating ordinal scales as ordinal scales. Nurs Res. 1993;42(3):184-186.
- Carifio J, Perla R. Resolving the 50-year debate around using and misusing Likert scales. Med Educ. 2008;42(12):1150-1152. doi:10.1111/j.1365-2923.2008.03172.x
- Kero P, Lee D. Likert is Pronounced “LICK-urt” not “LIE-kurt” and the Data are Ordinal not Interval. J Appl Meas. 2016;17(4):502-509.
- Norman G. Likert scales, levels of measurement and the “laws” of statistics. Adv Health Sci Educ Theory Pract. 2010;15(5):625-632. doi:10.1007/s10459-010-9222-y
- Paul Velleman and Leland Wilkinson 1993 Nominal, Ordinal, Interval, and Ratio Typologies are Misleading
